Três molas idênticas, de massas desprezíveis e comprimentos naturais , são dispostas verticalmente entre o solo e o teto a de altura. Conforme a figura, entre tais molas são fixadas duas massas pontuais iguais.
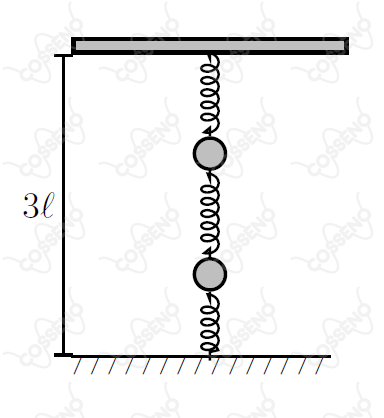
Na situação inicial de equilíbrio, retira-se a mola inferior (ligada ao solo) resultando no deslocamento da massa superior de uma distância para baixo, e da inferior, de uma distância também para baixo, alcançando-se nova posição de equilíbrio. Assinale a razão .
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Para entender melhor o comportamento do sistema com três molas, o ideal é imaginar que o sistema seja levado ao momento de equilíbrio a partir da posição em que as três molas estão com comprimento natural. A cada deslocamento feito pela esfera de cima e pela esfera de baixo, a mola central apenas se translada, sem mudar seu comprimento total. De fato, se a mola de cima muda de $\ell$ para $\ell + \Delta x_1$ e a de baixo de $\ell$ para $\ell - \Delta x_1$, a soma dos comprimentos das molas continua $3 \ell$. Portanto, a mola do meio não interfere nas forças.
Temos então, analisando a massa superior: $$F_e = P \Rightarrow kx_1 = mg \Rightarrow x_1 = mg/k$$
Após retirar a mola inferior, a massa superior se desloca de uma distância $d_1$ e a massa inferior se desloca de uma distância $d_2$. Ou seja, a mola de cima fica com um comprimento $\ell + x_1 + d_1$ e a mola do meio fica com um comprimento de $d_2 - d_1$.
Analisando as forças novamente na massa superior: $$F_{mola-superior} = P + F_{mola-meio}$$ $$k(x_1 + d_1) = mg + k(d_2 - d_1) \Rightarrow mg + kd_1 = mg + kd_2 - kd_1 \Rightarrow d_2 = 2d_1$$ $$Letra \ A$$

