$\cdot\ Resolução\ I$ 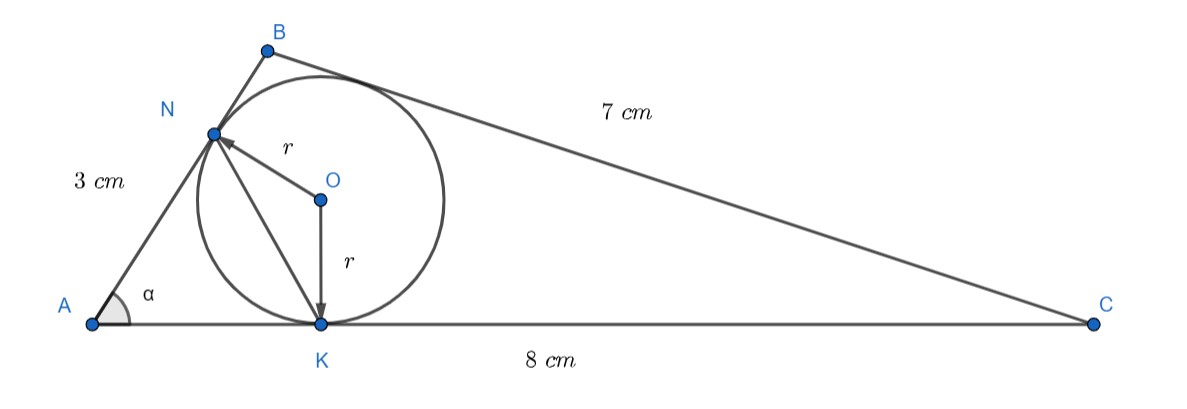A questão pode ser facilmente resolvida através da utilização de fórmulas para área de um triângulo, são elas: $\cdot\ $Fórmula de Heron: $$A=\sqrt{p(p-a)(p-b)(p-c)},\ p=\dfrac{a+b+c}{2}\text{ e } a,\ b,\ c\ \text{representam os lados do triângulo}$$ $\cdot\ $ Fórmula do radio da circunferência inscrita: $$A=p\cdot r,\ \text{onde }r\ \text{representa o raio da circunferência inscrita}$$ Igualando ambas as fórmulas obtemos o raio da circunferência inscrita: $$\sqrt{p(p-a)(p-b)(p-c)}=p\cdot r\Longrightarrow r=\dfrac{2}{\sqrt{3}}$$ Devemos agora encontrar o valor do ângulo $BÂC$, para isso, vamos utilizar a lei dos cossenos: $$\cos(BÂC)=\dfrac{AB^2+AC^2-BC^2}{2AC\cdot AB}=\dfrac{1}{2}\therefore BÂC=60^°$$ Como o ângulo $NÔK=180^°-BÂC,\ \cos (NÔK) = -\dfrac{1}{2}$ e que $O\widehat{N}K=30^°$, por fim, observando a figura, temos que $NK=2r\cos(30^°)=2$ $\cdot\ Resolução\ II$ 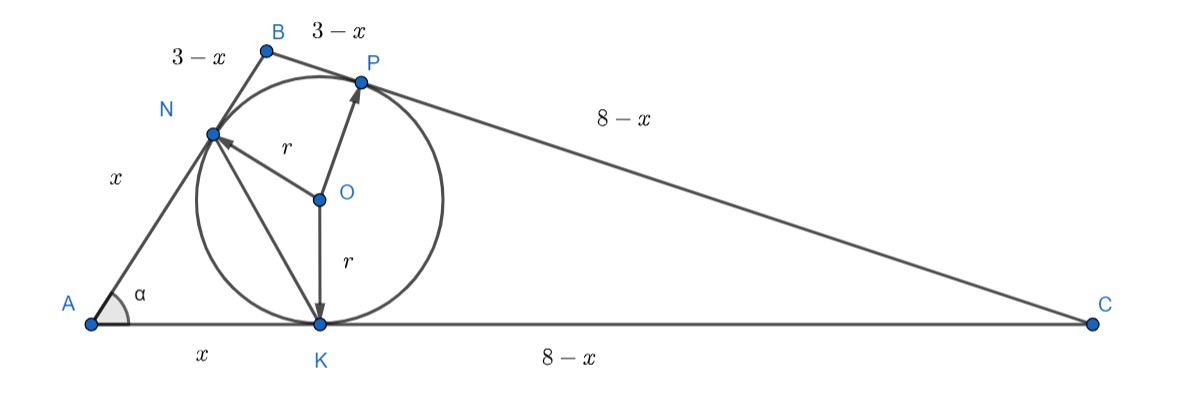Poderíamos chamar $AK$ de $x$ e portanto $KC=8-x=CP, \ BP=3-x=BN$ e $AN=x$, logo $\Delta ANK$ é isósceles. Realizando a lei dos cossenos para descobrir o valor de $BÂC$, encontramos: $$\cos(BÂC)=\dfrac{AB^2+AC^2-BC^2}{2AC\cdot AB}=\dfrac{1}{2}\therefore BÂC=60^°$$ Logo, $\Delta ANK$ é equilátero e como sabemos $BC=CP+ BP=3-x+8-x=7\Longrightarrow x=2\therefore\ NK=2$ $$Letra\ A$$