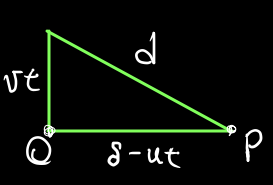
Ao passar pelo ponto , um helicóptero segue na direção norte com velocidade constante. Nesse momento, um avião passa pelo ponto , a uma distância de , e voa para o oeste, em direção a , com velocidade também constante, conforme mostra a figura.

Considerando o instante em que a distância entre o helicóptero e o avião for mínima, assinale a alternativa correta.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Ampliar Imagem

