Um elevador sobe verticalmente com aceleração constante e igual a . No seu teto está preso um conjunto de dois sistemas massa-mola acoplados em série, conforme a figura.
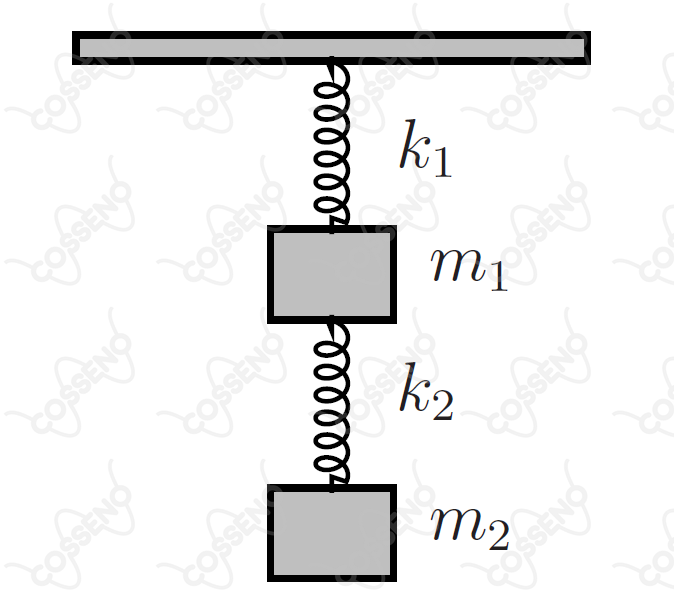
O primeiro tem massa e constante de mola , e o segundo, massa e constante de mola . Ambas as molas têm o mesmo comprimento natural (sem deformação) . Na condição de equilíbrio estático relativo ao elevador, a deformação da mola de constante é , e a da outra, . Pode-se então afirmar que é
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Escrevendo as leis de Newton para cada bloco:
$\text{Bloco 1:}$ $$k_{1}y - m_{1}g - k_{2}x = m_{1}a$$
$\text{Bloco 2:}$ $$k_{2}x - m_{2}g = m_{2}a.$$
Com isso, temos
$$x = \dfrac{m_{2}(g+a)}{k_{2}}$$
$$y = \dfrac{(m_{1} + m_{2)}(g+a)}{k_{1}}.$$
Portanto,
$$y - x = \dfrac{[(k_{2} - k_{1})m_{2} + k_{2}m_{1}](g+a)}{k_{1}k_{2}}.$$
Apriori note que para um refencial não inercial dentro do elevador a aceleração resultante atuante é igual a $(g+a )$.
Analisando as forças atuantes sobre os blocos dentro desse referencial e sabendo da condição de equilíbrio estático podemos constatar que
$\begin{cases}
k_{1}y= m_{1}(a+g) + k_{2}x
\\
k_{2}x = m_{2}(a+g)
\end{cases}$
$\implies k_{1}y= m_{1}(a+g) +m_{2}(a+g) \implies \boxed{y = \dfrac{(g+a)(m_{1} +m_{2})}{k_{1}}}$
$k_{2}x = m_{2}(a+g) \implies \boxed{x = \dfrac{m_{2}(g + a)}{k_{2}}}$
$\therefore$
$(y - x) = \dfrac{(g+a)(m_{1} +m_{2})}{k_{1}} - \dfrac{m_{2}(g + a)}{k_{2}}$
$= (g+a)\left(\dfrac{(m_{1} + m_{2})k_{2} - m_{2}k_{1}}{k_{1}k_{2}}\right)$
$ = \boxed{(y-x) = \left[\dfrac{(k_{2} - k_{1})m_{2}+ k_{2}m_{1}}{k_{1}k_{2}}\right] (g+a)}$
$\textbf{Resposta : Alternativa C}$


