Dos alunos de um colégio, cada um estuda pelo menos uma das três matérias:
Matemática, Física e Química. Sabe-se que dos alunos estudam Matemática, estudam Química e estudam Física. Sabe-se, ainda, que dos alunos estudam apenas Física e Matemática, enquanto estudam todas as três matérias. Os alunos que estudam apenas Química e Física mais aqueles que estudam apenas Matemática e Química totalizam estudantes. Determine .
CossenoGPT
Teste
gratuitamente agora
mesmo! 
Conforme as informações do enunciado, pode-se esboçar por $\text{Diagramas de Venn}$:
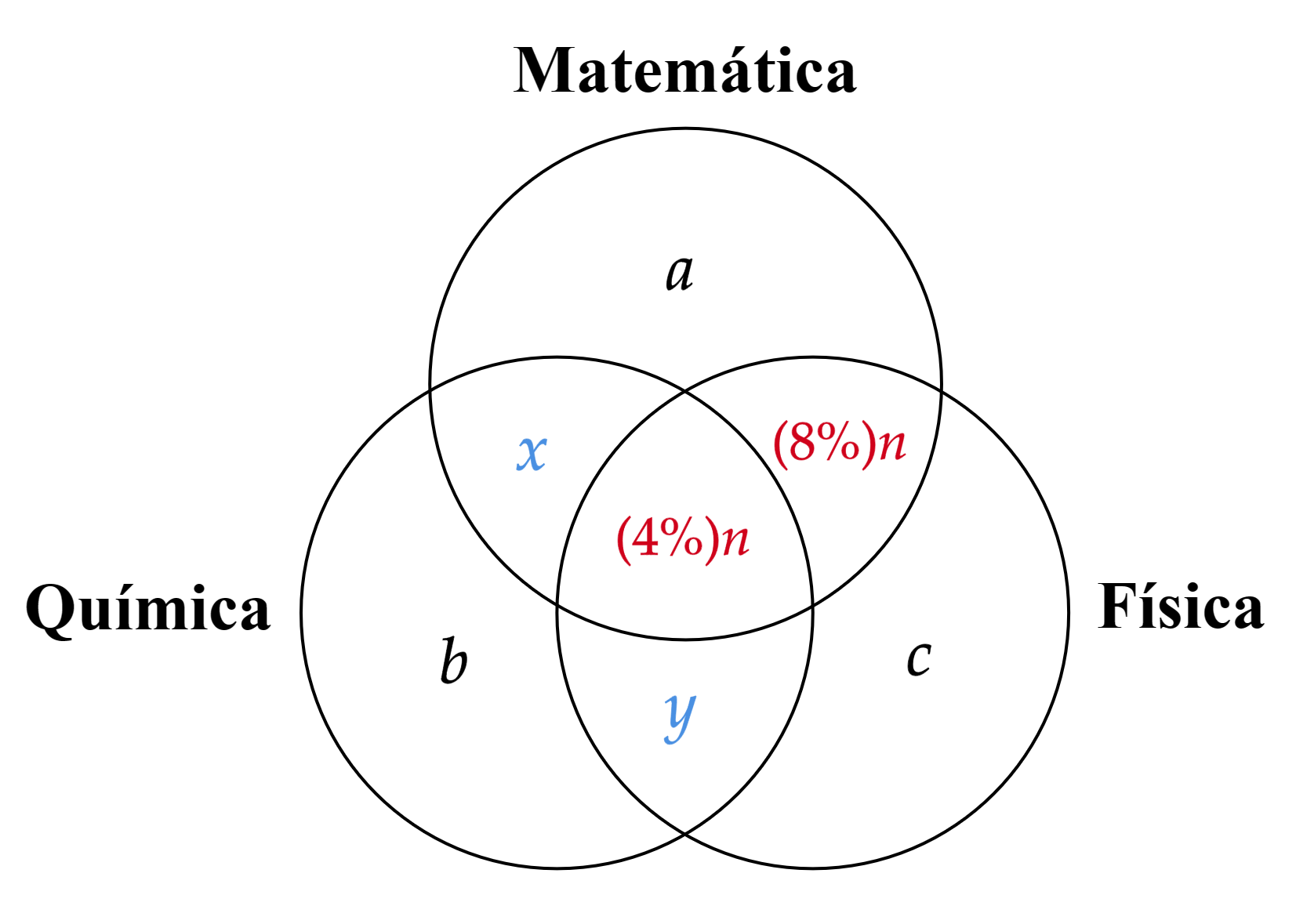Em que,\begin{cases}
\ \ \ \ 63&= x+y \\
(48\%)n &=a+x+ (12\%)n \\
(32\%)n &= x+y+b +(4\%)n \\
(36\%)n &= y+c+ (12\%)n\\
(100\%)n &= x+y+a+b+c +(12\%)n
\end{cases}Observe que somando as três linhas intermediárias, tem-se:\begin{matrix}
(48\%+32\%+ 36\%)n = (x+y+a+b+c) + (x+y) + (12\% + 4\% + 12\%)n
\end{matrix}Ou seja,\begin{matrix}
(88\%)n =(x+y+a+b+c) + (x+y)
\end{matrix}Substituindo a primeira e a última linha na expressão acima, segue:\begin{matrix}
(88\%)n = (88\%)n + 63
\end{matrix}Conclui-se então que caímos num absurdo, visto que $63 \ne 0$. Em outras palavras, não existe $n$ que satisfaça o problema.\begin{matrix}
\nexists \ n &\tiny{\blacksquare}
\end{matrix}
Ampliar Imagem
