A princípio, sabemos que a equação do enunciado representa uma circunferência, ou seja, podemos começar reduzindo a equação, veja:\begin{matrix} x^2 + \dfrac{m}{36}x + y^2 + \dfrac{m}{36}y - \dfrac{23}{36} = 0 \end{matrix}Então,\begin{matrix} \left(x^2 + \dfrac{m}{36}x \ {\color{#3368b8}{+ \dfrac{m^2}{2^2 \cdot 36^2}}}\right) {\color{#3368b8}{- \dfrac{m^2}{2^2 \cdot 36^2}}} + \left(y^2 + \dfrac{n}{36}y \ {\color{orangered}{+ \dfrac{n^2}{2^2 \cdot 36^2}}}\right) {\color{orangered}{- \dfrac{n^2}{2^2 \cdot 36^2}}} = \dfrac{23}{36} \end{matrix}Continuando,\begin{matrix} \left( x + \dfrac{m}{2\cdot 36}\right)^2 + \left( y + \dfrac{n}{2\cdot 36}\right)^2 = \dfrac{23}{36} + \dfrac{m^2 + n^2}{2^2 \cdot 36^2} \end{matrix}Segundo o enunciado, o raio da circunferência é $1$, consequentemente:\begin{matrix} \dfrac{23}{36} + \dfrac{m^2 + n^2}{2^2 \cdot 36^2} = 1 \end{matrix}A partir da relação do enunciado entre $m$ e $n$, pode-se isolar uma das incógnitas - façamos isso com $m$ - logo:\begin{matrix}n = \pm 36\end{matrix}Lembre-se que o centro $C$ está no segundo quadrante, por isso, a raiz positiva de $n$ não satisfaz a situação do enunciado. Nesse sentido, têm-se:\begin{matrix} n = 36 &,& m = -\dfrac{2}{3}\cdot 36 \end{matrix}Com isso, a equação fica:\begin{matrix} \left( x + \dfrac{1}{3}\right)^2 + \left( y + \dfrac{1}{2}\right)^2 =1 &,& C: \left(-\dfrac{1}{3} , \dfrac{1}{2}\right) \end{matrix}Agora, resta-nos encontrar $A$ e $B$ e calcular a área do triângulo. Conforme enunciado, $A$ e $B$ se encontram em $Oy$, ou seja, podemos encontrá-los simplesmente fazendo $x = 0$ na equação da circunferência. Todavia, isto não é necessário, pois sabemos que o triângulo é necessariamente isósceles - os pontos de intersecção fazem parte da circunferência - com $\overline{AC} = \overline{BC} = r$, assim como conhecemos a altura do triângulo em relação a base $\overline{AB}$, que é simplesmente $|-1/3|$, veja abaixo: 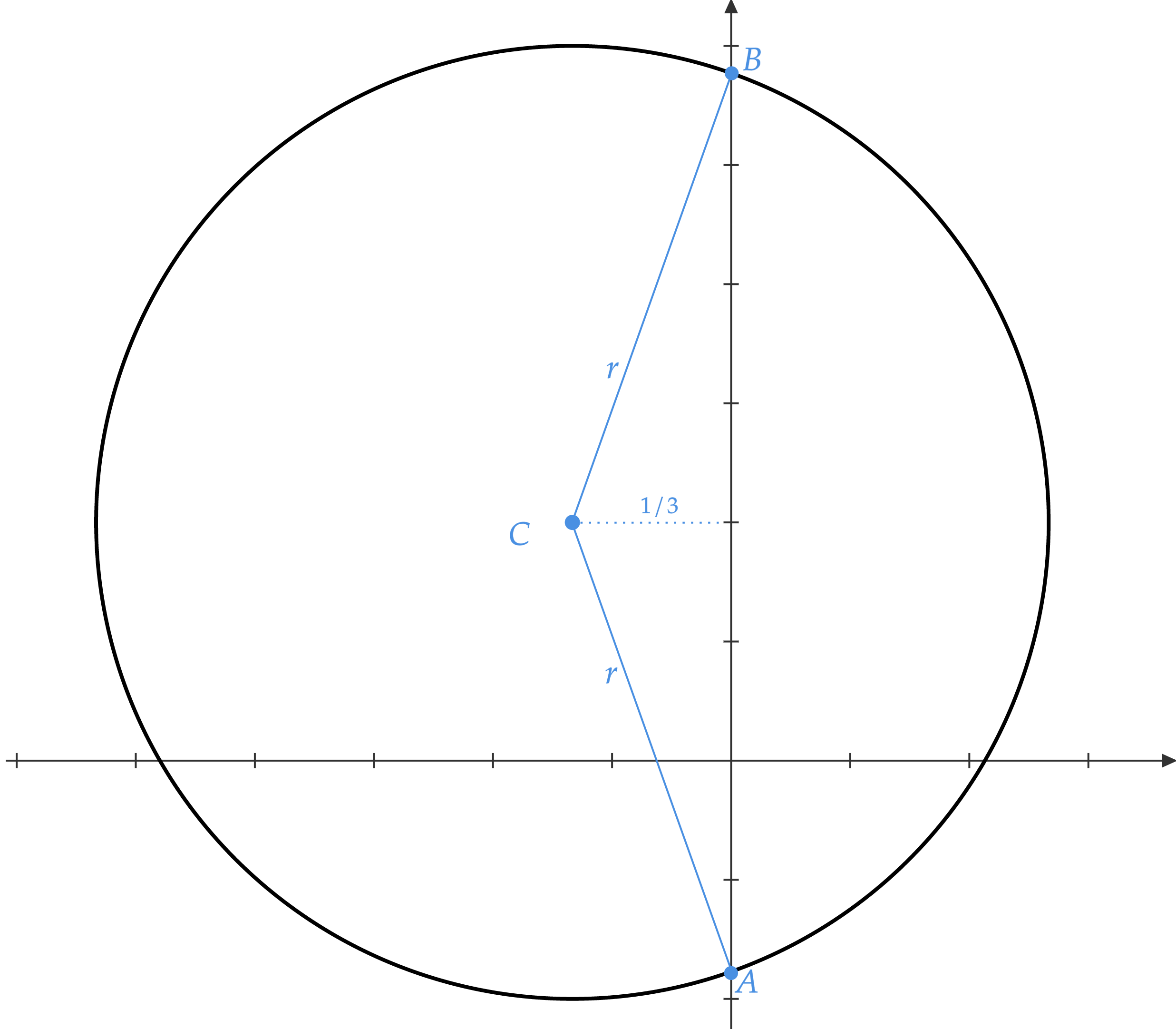A partir daqui existem diversas formas de encontrar a área, você pode, por exemplo, encontrar os pontos $A$ e $B$, e assim encontrar a área por pura geometria analítica - algoritmo de área -, ou simplesmente fazer o seguinte: aplicar o teorema de Pitágoras como abaixo:\begin{matrix} r^2 = \left(\dfrac{1}{3}\right)^2 + \left(\dfrac{\overline{AB}}{2}\right)^2 &\therefore& \bigg|\dfrac{\overline{AB}}{2}\bigg| = \dfrac{2\sqrt{2}}{3} \end{matrix}Portanto, a área do triângulo é:\begin{matrix} [ABC] = 2 \left(\dfrac{ \dfrac{2\sqrt{2}}{3} \cdot \dfrac{1}{3}}{2}\right) = \dfrac{2\sqrt{2}}{9} \ \ \tiny{\blacksquare} \end{matrix}\begin{matrix}Letra \ (D) \end{matrix}