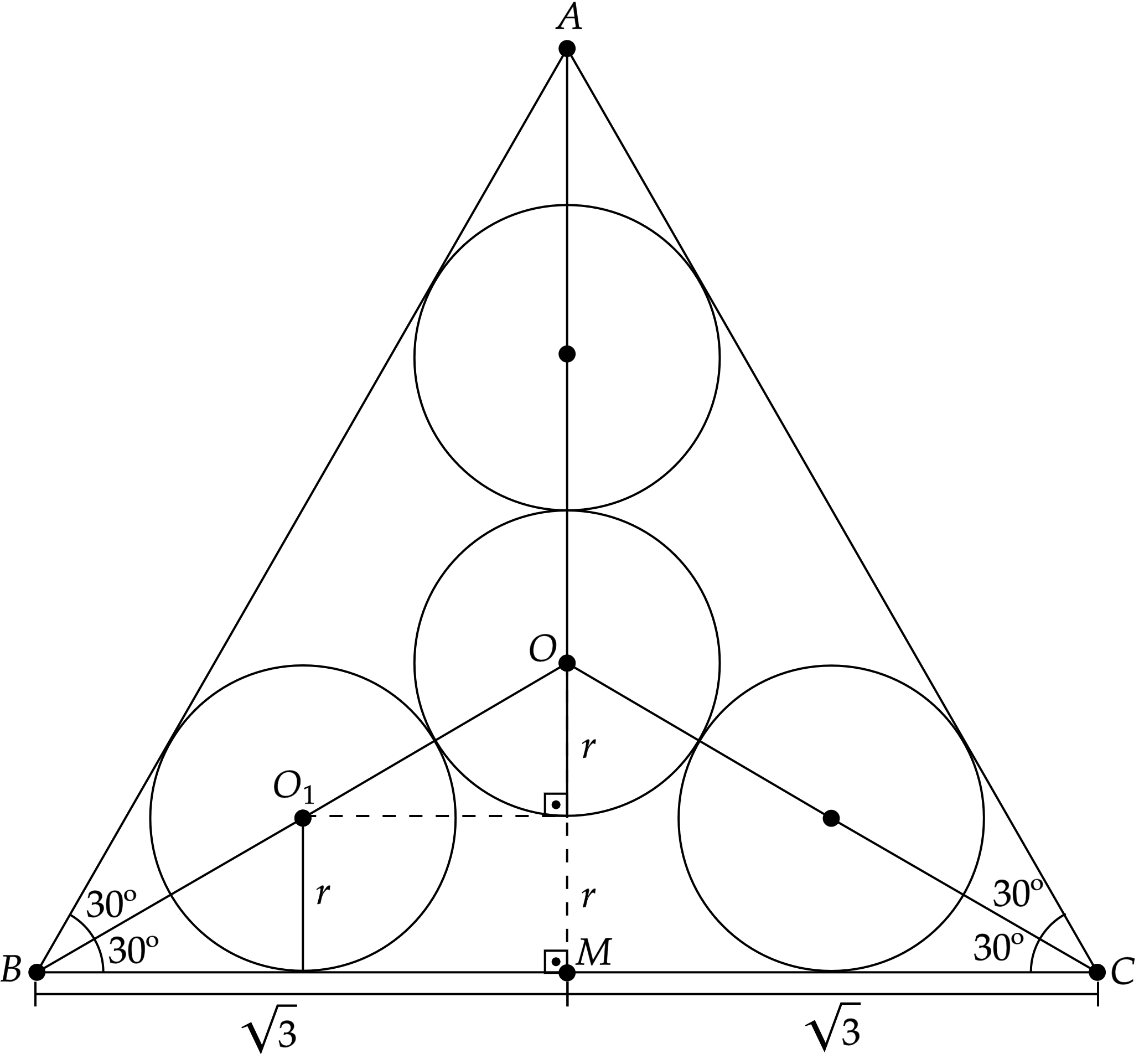
A princípio, note que o triângulo é equilátero, ou seja, seu circuncentro coincide com o incentro, baricentro e ortocentro. Nesse sentido, podemos esboçar a situação como: $• \ \text{a)}$ $\color{#3368b8}{\text{r = 1/2 cm}}$ Repare no triângulo $AOM$, por trigonometria, têm-se:\begin{matrix} \tan{30º} = \dfrac{2r}{\sqrt{3}} &\therefore& r = \dfrac{1}{2} \ \pu{cm} \ \ \tiny{\blacksquare} \end{matrix}$• \ \text{b)}$ $\color{#3368b8}{S = (3\sqrt{3} - \pi) \ \pu{cm^2}}$ Pondere que a área do triângulo não preenchida pelos círculos é simplesmente a área do triângulo menos as dos quatro círculos. Dessa forma, para área do triângulo equilátero, pode-se escrever:\begin{matrix} [ABC] = \dfrac{(2\sqrt{3})^2\sqrt{3}}{4} &\therefore& [ABC] = 3\sqrt{3} \ \pu{cm^2} \end{matrix}Conhecido o raio dos círculos, têm-se para cada um:\begin{matrix} [O] = \pi r^2 &\therefore& [O] = \dfrac{\pi}{4} \end{matrix}Com isso, a área $S$ solicitada é:\begin{matrix} S = [ABC] - 4[O] &\therefore& S = (3\sqrt{3} - \pi) \ \pu{cm^2} \ \ \tiny{\blacksquare} \end{matrix}$• \ \text{c)}$ $\color{#3368b8}{\text{d = 1 cm}}$ Observe que a distância $d$ solicitada é simplesmente $\overline{BC_1}$, esta que também pode ser encontrada por trigonometria:\begin{matrix}\sin{30º} = \dfrac{r}{d} &\therefore& d= 1 \ \pu{cm} \ \ \tiny{\blacksquare} \end{matrix}