A princípio, a questão trata sobre $\text{as raízes da unidade}$. Nesse contexto, deve-se saber que as raízes de $z^n = 1$ representam os vértices de um polígono convexo de $n$ lados, sendo $|z_{k+1} - z_{k}|$, com $k = 1,2,\dots , n$ os lados do polígono no plano de Argand-Gauss. Resumindo, o enunciado nos solicita a quantidade de distâncias com comprimentos distintos entre os complexos $z_i$ e $z_j$, ou seja, o problema agora é apenas combinatória. No caso, vamos pensar num afixo qualquer, seja ele $z_k$, a distância deste para os demais afixos varre todas as distâncias distintas, isto é:\begin{matrix} |z_k -z_1| \ne |z_k - z_2| \ne \dots \ne |z_k - z_n| \end{matrix}Com isso, de quantas formas podemos vincular $z_k$ ao demais afixos? Ora, não podemos vincular $z_k$ à ele mesmo, então nos restam $n-1$ afixos para vincular. Contudo, precisamos tomar cuidado com a simetria do problema, fazendo isso estamos varrendo todas as distâncias distintas, porém, também estamos computando pares iguais! Observe a figura abaixo: 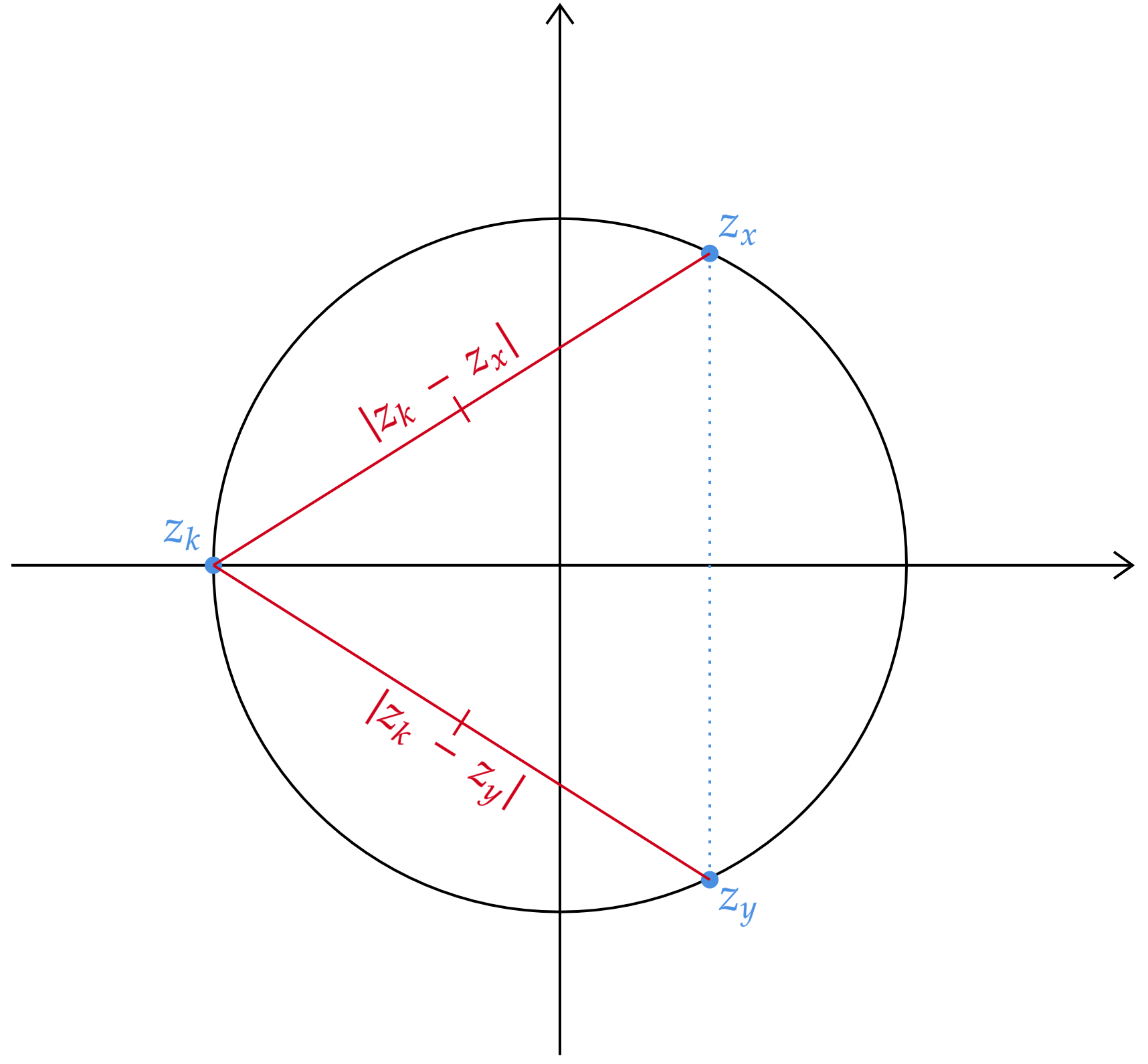Veja que para cada afixo $z_x$, existe um afixo $z_y$ simetricamente oposto a ele, conferindo dois comprimentos idênticos. Felizmente, resolver isso é simples, pois, se $n-1$ representa o dobro do número de comprimentos distintos, encontrar apenas os comprimentos distintos é o mesmo que fazer:\begin{matrix} \dfrac{n-1}{2} \ \ \ \tiny{\blacksquare} \end{matrix}