Sejam um quadrado e um ponto sobre . Considere as áreas do quadrado , do trapézio e do triângulo . Sabendo que estas áreas definem, na ordem em que estão apresentadas, uma progressão aritmética cuja soma é , a medida do segmento , em , é igual a
CossenoGPT
Teste
gratuitamente agora
mesmo! 
Comecemos por esboçar a situação:
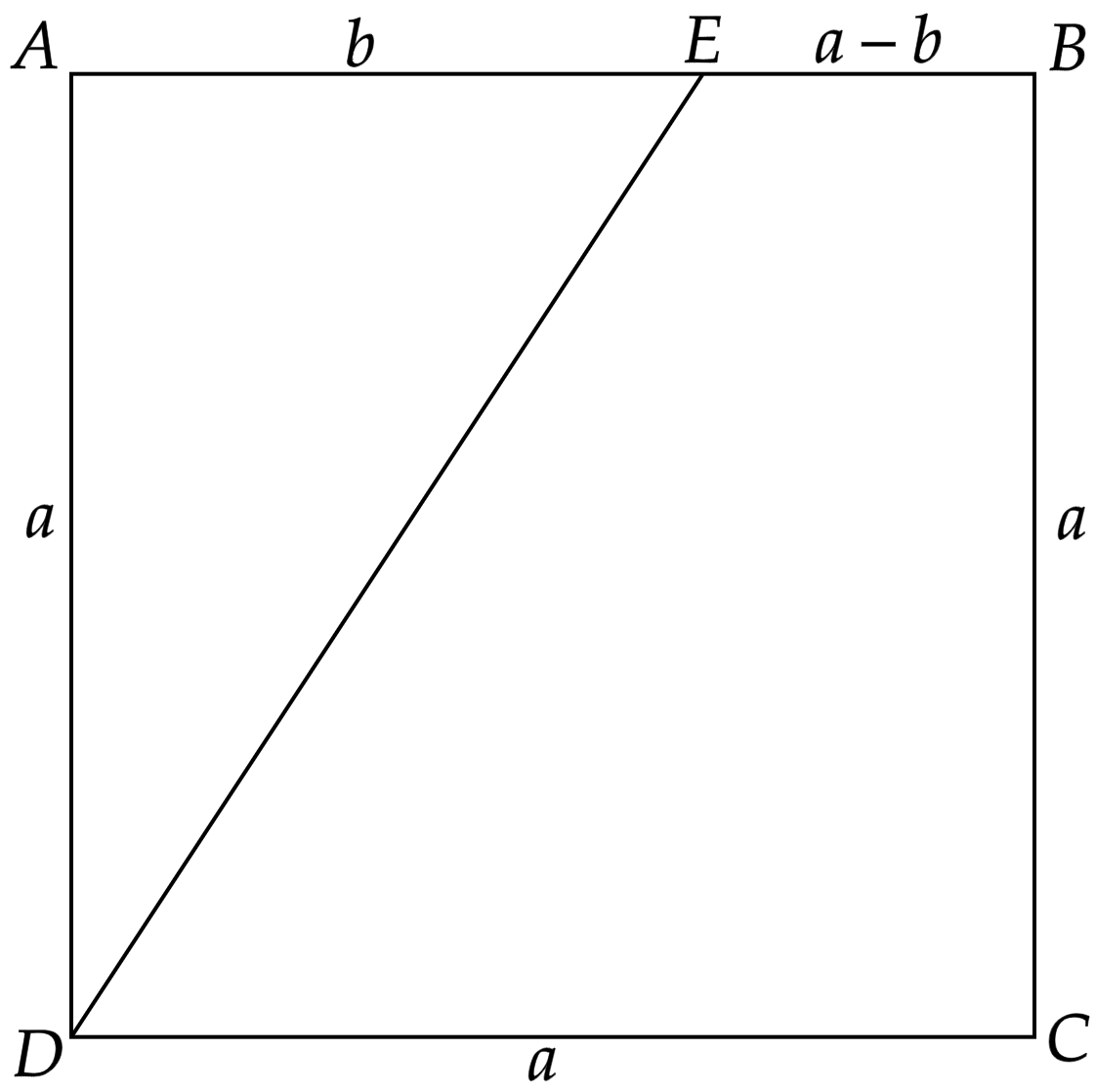Segundo enunciado, temos a progressão:\begin{matrix}
[ABCD] &,& [BEDC] &,& [ADE]
\end{matrix}O que equivale escrever:\begin{matrix}
a^2 &,& \dfrac{(2a-b)a}{2} &,& \dfrac{ab}{2}
\end{matrix}Conforme progressão, é possível escrever:\begin{matrix}
\dfrac{(2a-b)a}{2} = \dfrac{a^2 + \dfrac{ab}{2}}{2} &\therefore& b = \dfrac{2a}{3}
\end{matrix}Consequentemente, pensando na soma da progressão:\begin{matrix}
a^2 + \dfrac{\left(2a-\dfrac{3a}{2}\right)a}{2} + \dfrac{a\left(\dfrac{3a}{2}\right)}{2} = 200 &\therefore& a = 10 \ \pu{cm}
\end{matrix}Desse modo,\begin{matrix}
b = \dfrac{20}{3} \ \pu{cm}
\end{matrix}\begin{matrix}Letra \ (C)
\end{matrix}
Ampliar Imagem
