Um quadro quadrado de lado e massa , feito de um material de coeciente de dilatação superficial , é pendurado no pino por uma corda inextensível, de massa desprezível, com as extremidades fixadas no meio das arestas laterais do quadro, conforme a figura. A forca de tração maxima que a corda pode suportar é . A seguir, o quadro é submetido a uma variação de temperatura , dilatando.
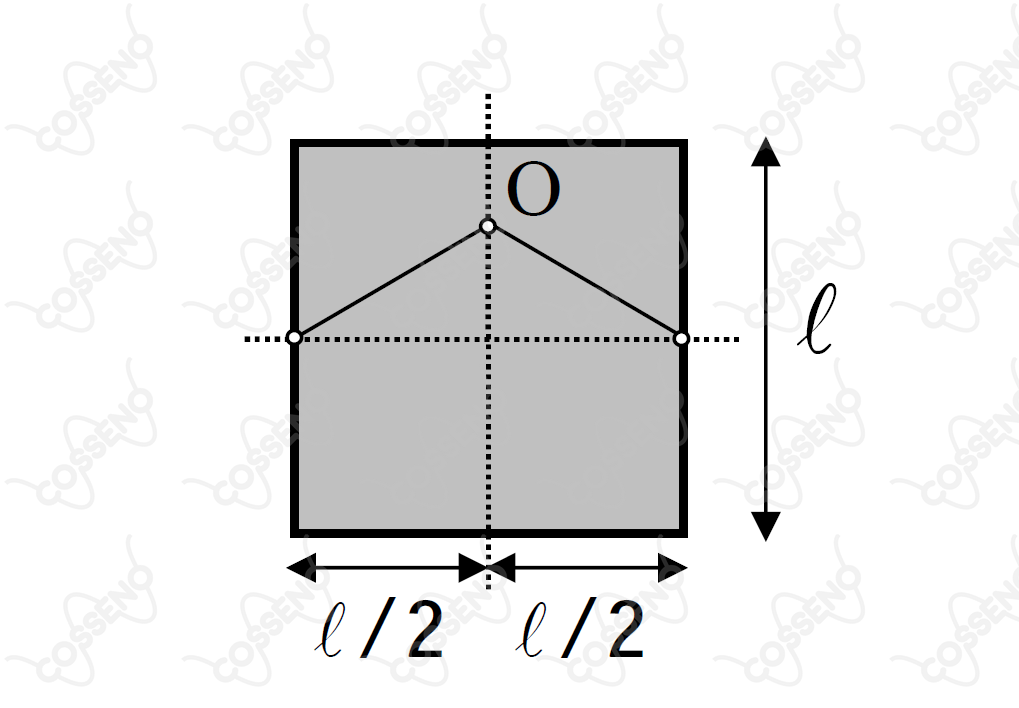
Considerando desprezível a variação no comprimento da corda devida a dilatação, podemos afirmar que o comprimento mínimo da corda para que o quadro possa ser pendurado com segurança é dado por
CossenoGPT
Teste
gratuitamente agora
mesmo! 
Começando a análise pensando na dilatação, vamos assumir que o material é homogêneo, assim, após $ℓ$ dilatar até $L$, têm-se superficialmente:\begin{matrix}
L^2 = ℓ^2(1 + \beta \Delta T)
\end{matrix}Não se esqueça que o quadro é um quadrado, assim, podemos esboçar a situação como:
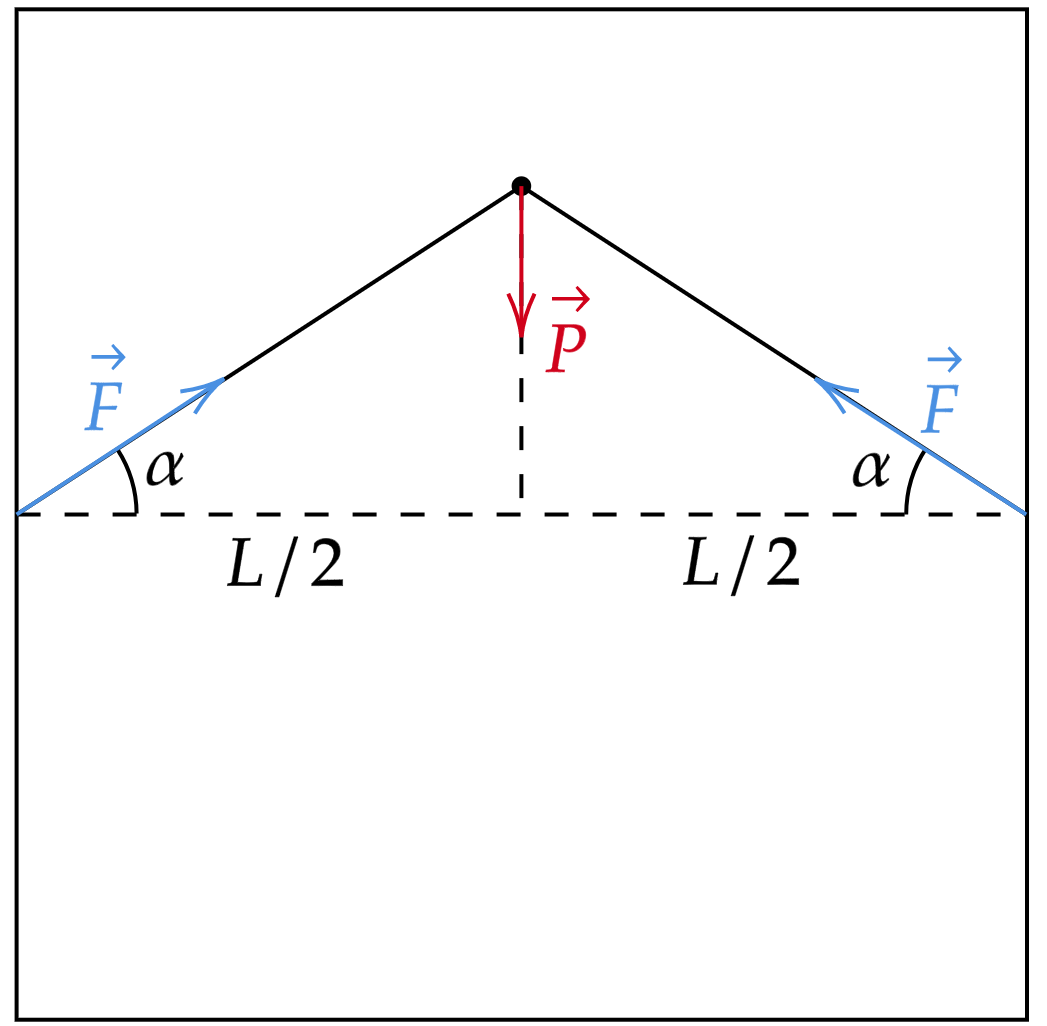A priori, podemos decompor as forças de tração máxima $F$ visando o equilíbrio vertical, ou seja:\begin{matrix}
2F\sin{\alpha} = P &\therefore& \sin{\alpha} = \dfrac{mg}{2F}
\end{matrix}Por outro lado, olhando para trigonometria do problema,\begin{matrix}
\cos{\alpha} = \dfrac{(L/2)}{(x/2)} = \dfrac{L}{x} &,& \text{comprimento da corda} := x
\end{matrix}Agora, relacionando os resultados anteriores conforme equação fundamental da trigonometria:\begin{matrix}
\sin^2{\alpha} + \cos^2{\alpha} = 1
\end{matrix}Consequentemente,\begin{matrix}
\left(\dfrac{mg}{2F} \right)^2 + \left(\dfrac{L}{x} \right)^2 = 1
\end{matrix}Portanto,\begin{matrix}
x = 2ℓF \sqrt{\dfrac{1 + \beta \Delta T}{4F^2 - m^2g^2}} \ \ \tiny{\blacksquare}
\end{matrix}\begin{matrix}Letra \ (E)
\end{matrix}
Ampliar Imagem
