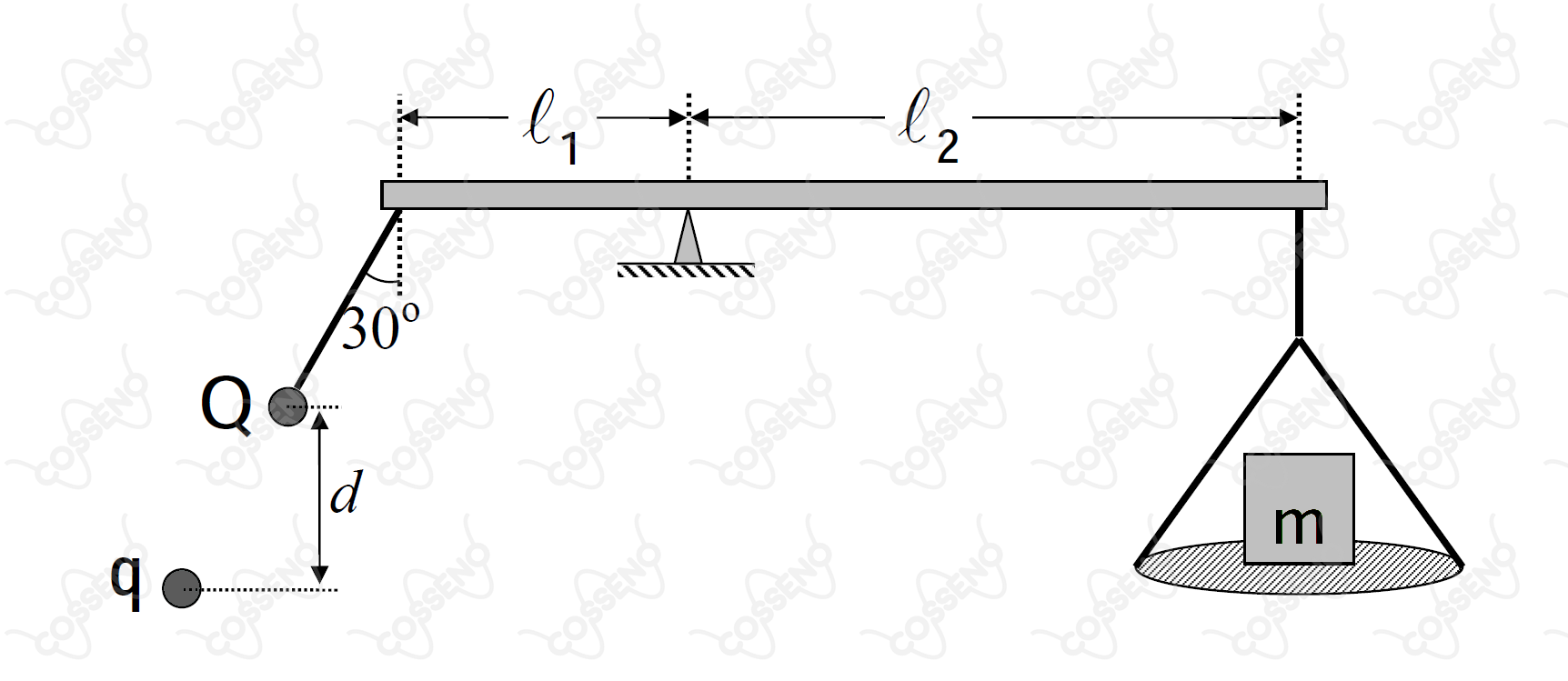
Considere uma balança de braços desiguais, de comprimentos e , conforme mostra a figura. No lado esquerdo encontra-se pendurada uma carga de magnitude e massa desprezível, situada a uma certa distância de outra carga, . No lado direito encontra-se uma massa sobre um prato de massa desprezível. Considerando as cargas como pontuais e desprezível a massa do prato da direita, o valor de para equilibrar a massa é dado por
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A princípio, observe que há duas forças atuando na barra - excepcionando o ponto de contato -, a força de tração exercida pela interação elétrica entre as cargas, e o peso do corpo de massa $m$. Nesse sentido, podemos começar calculando a força de interação entre as cargas, vamos assumir que a distância entre elas é $x$, logo, conforme geometria do problema:\begin{matrix}
\cos{30º} = \dfrac{d}{x} &\therefore& x = \dfrac{2}{\sqrt{3}}d
\end{matrix}Com isso, a força elétrica deve de ser:\begin{matrix}
F_{ele} = \dfrac{k_0 |Q||q|}{x^2} &\therefore& F_{ele} = \dfrac{3k_0 |Q||q|}{4d^2}
\end{matrix}Decompondo esta força na vertical, e analisando o momento dela, assim como do peso $m$ em relação ao ponto de contato, têm-se:\begin{matrix}
\left(\dfrac{3k_0 |Q||q|}{4d^2} \cos{30º}\right) \cdot ℓ_1 = (mg) \cdot ℓ_2
\end{matrix}Portanto,\begin{matrix}
q = -\dfrac{8mgℓ_2 d^2}{3\sqrt{3} k_0 Q ℓ_1} \ \ \tiny{\blacksquare}
\end{matrix}\begin{matrix}Letra \ (E)
\end{matrix}
Apriori adote as cargas sendo cargas de sinais opostos.
Seja $T$ a tração da corda que pendura a carga de magnitude $Q$ e $\vec{F_{e}}$ a força eletrostática atuante sobre a carga $Q$ e sobre a carga $q$.
Calculando o módulo de $\vec{F_{e}}$ temos que
$F_{e} = k_{0} \cdot \dfrac{|Q||q|}{\left( \dfrac{d}{\cos30°}\right)^2} = F_{e} = \dfrac{3k_{0}|Q||q|}{4d^2}$
Note que $T = F_{e}$ , perceba também que o momento linear da força $T$ deve ser igual ao momento linear da força $mg$
$\therefore$
$T \cos30° \cdot L_{1}=mg \cdot L_{2} = \dfrac{3k_{0}|Q||q|}{4d^2} \cdot \dfrac{\sqrt{3}}{2} \cdot L_{1} = mg \cdot L_{2} $
$\implies |q| = \dfrac{8mgL_{2}d^2}{(3\sqrt{3}k_{0}|Q|L_{1})}$
Adotado a carga $q$ oposta à $Q$ , podemos escrever que
$\boxed{q= - \dfrac{8mgL_{2}d^2}{(3\sqrt{3}k_{0}QL_{1})}}$
$\textbf{Resposta : Alternativa E}$


