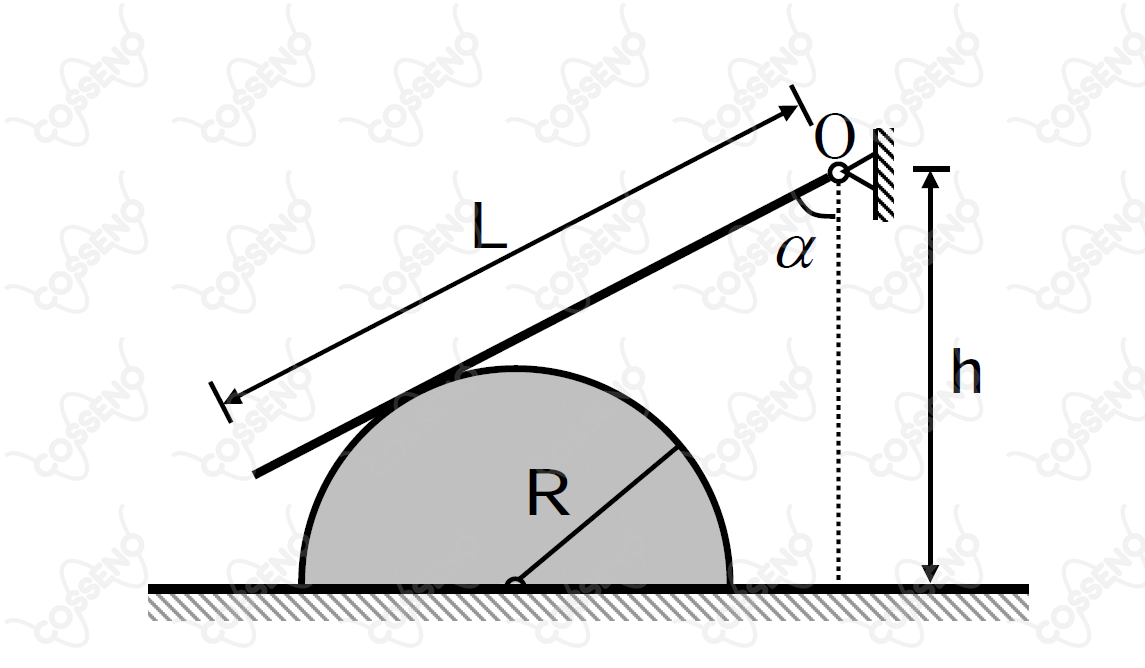
Considere um semicilindro de peso e raio sobre um plano horizontal não liso, mostrado em corte na figura. Uma barra homogênea de comprimento e peso está articulada no ponto . A barra esta apoiada na superfície lisa do semicilindro, formando um ângulo com a vertical. Quanto vale o coeficiente de atrito mínimo entre o semicilindro e o plano horizontal para que o sistema todo permaneça em equilíbrio?
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Primeiramente, comecemos por denotar a força de reação da barra empurrando o semicilindro de $F$. Por outro lado, iremos chamar a força de atrito de $f$. Dessa forma, analisando as forças que atuam no semicilindro, notamos quatro, a reação da barra, a reação do solo, o atrito, e claro, o peso do semicilindro. Não é difícil trabalhar este equilíbrio, vejamos:\begin{matrix}
\text{Horizontal:} & f &=& F\cos{\theta} \\ \text{Vertical:} & N &=&P + F\sin{\theta}
\end{matrix}Conhecido o conceito de atrito, sabemos que para o atrito estático máximo, têm-se:\begin{matrix} f = \mu N &\Rightarrow& F\cos{\theta} = \mu (P + F\sin{\theta}) &\therefore& \mu = \dfrac{\cos{\alpha}}{\dfrac{P}{F} + \sin{\alpha}} & \text{(I)}
\end{matrix}Observe que $F$ não consta nas alternativas, ou seja, precisamos substitui-la para algo em função dos outros termos presentes. Nesse sentido, podemos pensar no torque da barra, este deve ser nulo devido o equilíbrio, assim, analisemos a situação abaixo:
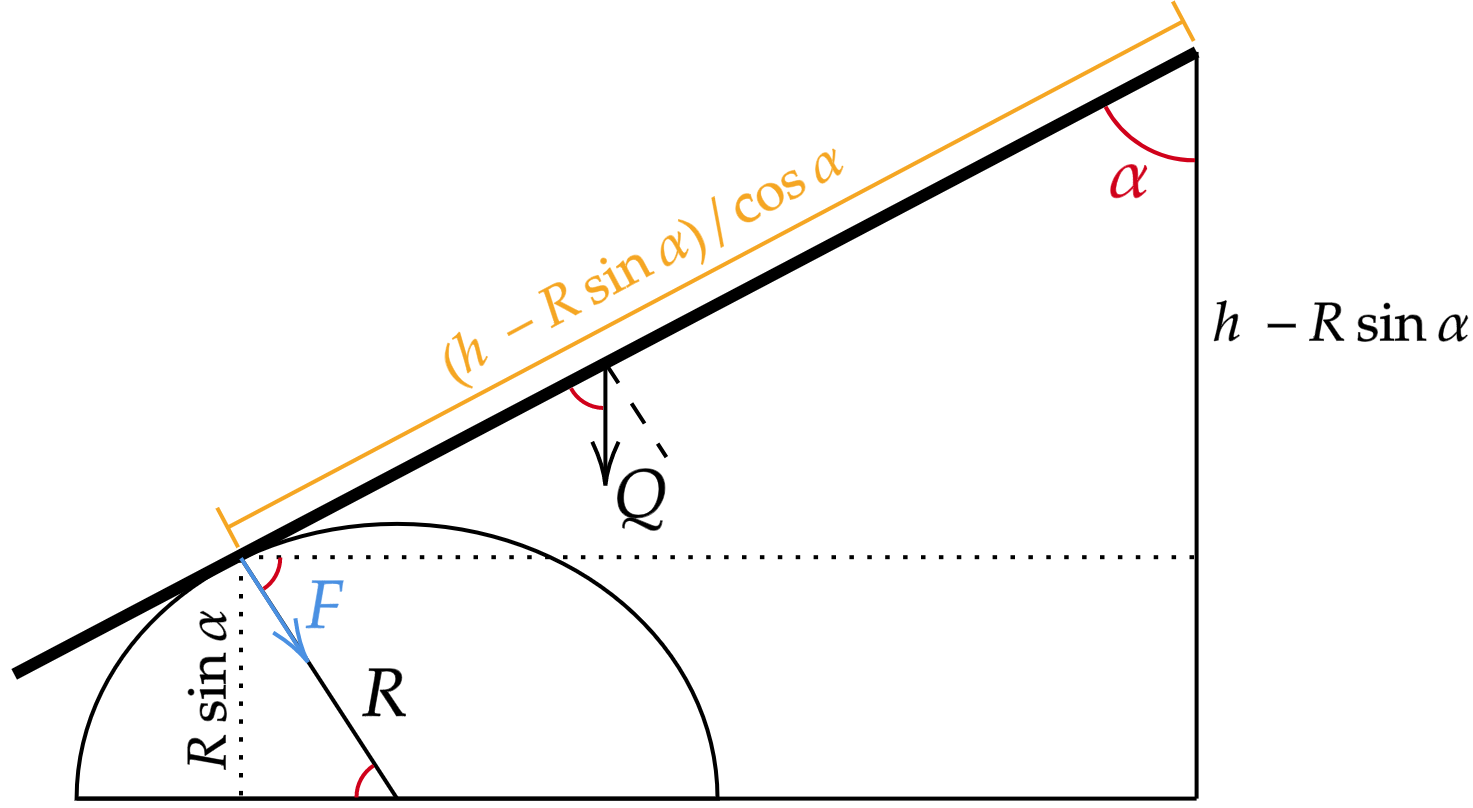 $\color{orangered}{\text{Obs:}}$ A força $F$ foi posta atuando no semicilindro a fim de facilitar a análise da geometria do problema, na barra o seu sentido é obviamente contrário ao da imagem.
Com isso, analisando o momento das forças da barra em relação ao ponto de articulação $O$, têm-se:\begin{matrix} F \cdot \left(\dfrac{h - R\sin{\alpha}}{\cos{\alpha}}\right) = (Q\sin{\alpha}) \cdot \dfrac{L}{2}
\end{matrix}Isolando $F$ na expressão acima e substituindo em $ \text{(I)}$, nota-se:\begin{matrix}
\mu = \dfrac{\cos{\alpha}}{\dfrac{2P(h - R\sin{\alpha})}{ (Q\sin{\alpha}) L\cos{\alpha}} + \sin{\alpha}}
\end{matrix}Consequentemente,\begin{matrix}
\mu = \dfrac{\cos{\alpha}}{2P\left( \dfrac{h}{LQ\sin{\alpha}\cos{\alpha}} - \dfrac{R}{LQ\cos{\alpha}}\right) + \sin{\alpha}}
\end{matrix}Conhecido o seno da soma, mais precisamente o arco-duplo:\begin{matrix}
\sin{2\alpha} = 2\sin{\alpha}\cos{\alpha}
\end{matrix}Portanto,\begin{matrix}
\mu = \dfrac{\cos{\alpha}}{2P\left( \dfrac{2h}{LQ\sin{2\alpha}} - \dfrac{R}{LQ\cos{\alpha}}\right) + \sin{\alpha}} & \tiny{\blacksquare}
\end{matrix}\begin{matrix}Letra \ (C)
\end{matrix}
$\color{orangered}{\text{Obs:}}$ A força $F$ foi posta atuando no semicilindro a fim de facilitar a análise da geometria do problema, na barra o seu sentido é obviamente contrário ao da imagem.
Com isso, analisando o momento das forças da barra em relação ao ponto de articulação $O$, têm-se:\begin{matrix} F \cdot \left(\dfrac{h - R\sin{\alpha}}{\cos{\alpha}}\right) = (Q\sin{\alpha}) \cdot \dfrac{L}{2}
\end{matrix}Isolando $F$ na expressão acima e substituindo em $ \text{(I)}$, nota-se:\begin{matrix}
\mu = \dfrac{\cos{\alpha}}{\dfrac{2P(h - R\sin{\alpha})}{ (Q\sin{\alpha}) L\cos{\alpha}} + \sin{\alpha}}
\end{matrix}Consequentemente,\begin{matrix}
\mu = \dfrac{\cos{\alpha}}{2P\left( \dfrac{h}{LQ\sin{\alpha}\cos{\alpha}} - \dfrac{R}{LQ\cos{\alpha}}\right) + \sin{\alpha}}
\end{matrix}Conhecido o seno da soma, mais precisamente o arco-duplo:\begin{matrix}
\sin{2\alpha} = 2\sin{\alpha}\cos{\alpha}
\end{matrix}Portanto,\begin{matrix}
\mu = \dfrac{\cos{\alpha}}{2P\left( \dfrac{2h}{LQ\sin{2\alpha}} - \dfrac{R}{LQ\cos{\alpha}}\right) + \sin{\alpha}} & \tiny{\blacksquare}
\end{matrix}\begin{matrix}Letra \ (C)
\end{matrix}

Ampliar Imagem