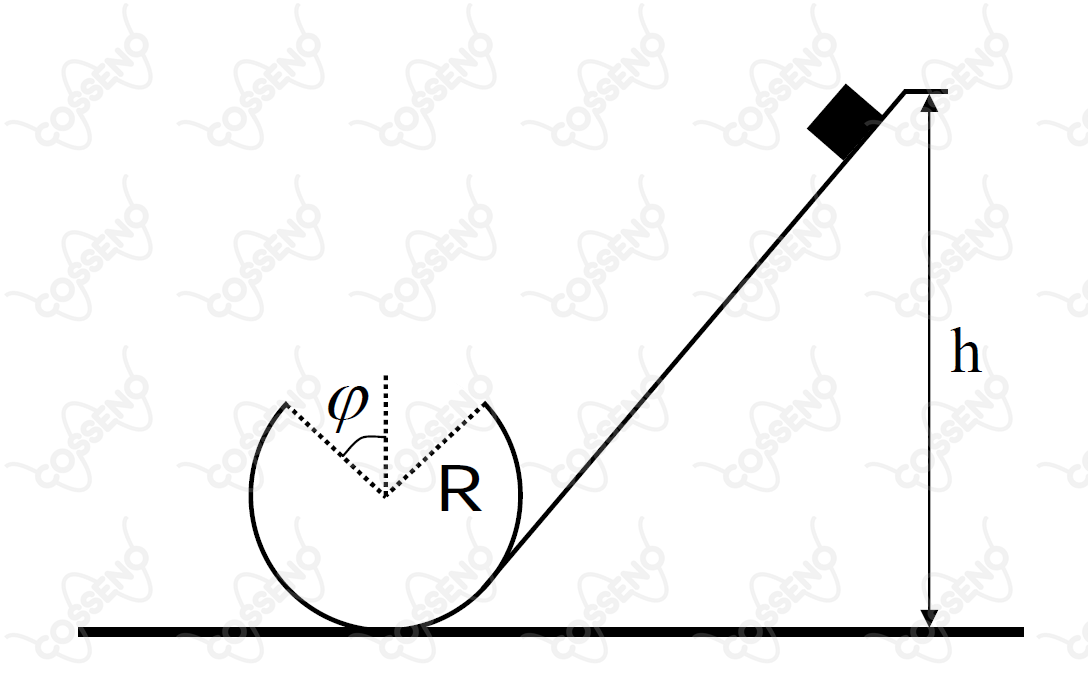
Um pequeno bloco desliza sobre uma rampa e logo em seguida por um "loop" circular de raio , onde há um rasgo de comprimento de arco , como ilustrado na figura. Sendo a aceleração da gravidade e desconsiderando qualquer atrito, obtenha a expressão para a altura inicial em que o bloco deve ser solto de forma a vencer o rasgo e continuar em contato com o restante da pista.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A ideia aqui é imaginar que o loop só passa a existir no momento que o corpo chegou no final da rampa. Caso contrário (pelo desenho) haveria um choque entre os dois.
Para passar o rasgo e continuar no loop, o corpo deverá percorrer uma trajetória parabólica cujo alcance é exatamente a distância entre os pontos em que ele perde e ganha contato. Essa distância é dada por $R\sin{\phi} + R\sin{\phi} = 2R\sin{\phi}$. Observe também que o ângulo de lançamento (ou seja o ângulo em relação à horizontal com o qual o corpo se desloca) é exatamente $\phi$ também. Assim, relembrando a expressão do alcance de um lançamento oblíquo: $$A = \dfrac{v^2 \cdot 2 \cdot \sin{\theta}\cdot\cos{\theta}}{g} \Rightarrow 2R\sin{\phi} = \dfrac{v^2 \cdot 2 \cdot \sin{\phi}\cdot\cos{\phi}}{g} $$Logo, $$v^2 = \dfrac{Rg}{\cos \phi}$$Ou seja, a expressão acima corresponde à velocidade que o corpo deve possuir no instante em que desgruda do loop e inicia o movimento aéreo.
Por fim, para descobrir a altura inicial de soltura na rampa, podemos utilizar a conservação da energia , pois não atuam forças dissipativas: $$mgh = mgH + \dfrac{mv^2}{2}$$onde $H$ é a altura no ponto em que o corpo se descola do loop, que, por geometria simples: $H = R + R\cos\theta$ Substituindo $H$ e $v^2$, obtém-se $$h = R \bigg(1 + \cos{\phi} + \dfrac{1}{2\cos{\phi}} \bigg)$$

20:20 05/11/2025
Eu não entendi porque essa resposta é valida, se para determinar a velocidade, vc pressupõe apenas que vença o rasgo e não vencer o rasgo e continuar em contato com a rampa, a velocidade mínima nesse caso não seria a altura máxima não passar da altura da rampa? Dessa forma garantindo que mantenha contato com a rampa

