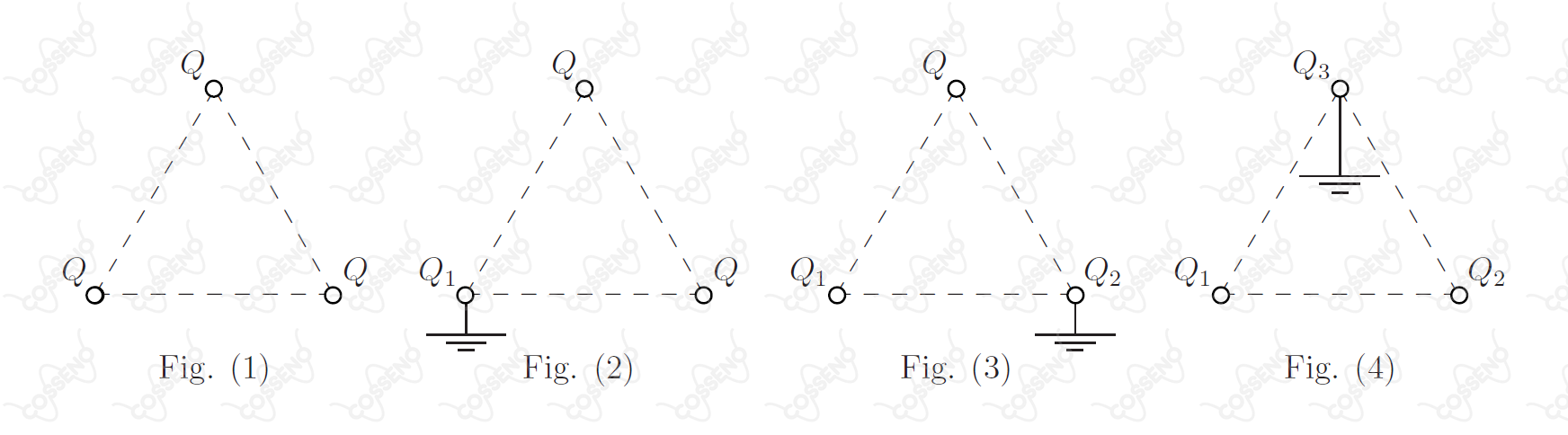
Três esferas condutoras, de raio a e carga , ocupam os vértices de um triângulo eqüilátero de lado , conforme mostra a figura ().
Considere as figuras (), () e (), em que, respectivamente, cada uma das esferas se liga e desliga da Terra, uma de cada vez. Determine, nas situações (), () e (), a carga das esferas , e , respectivamente, em função de e .
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Para cada situação, em algum momento é estabelecido um equilíbrio eletrostático, ou melhor, o momento em que o potencial induzido na carga aterrada é nulo. Por isso, tem-se para cada situação:
$• \ \text{Situação (I):}$ $\color{#3368b8}{Q_1 = -\dfrac{2Qa}{b}}$\begin{matrix}
\dfrac{KQ_1}{a} + \dfrac{KQ}{b} + \dfrac{KQ}{b} = 0 &\therefore& Q_1 = -\dfrac{2Qa}{b} & \tiny{\blacksquare}
\end{matrix}
$• \ \text{Situação (II):}$ $\color{#3368b8}{Q_2 = \dfrac{Qa}{b} \left(\dfrac{2a}{b} -1\right)}$\begin{matrix}
\dfrac{KQ_1}{b} + \dfrac{KQ_2}{a} + \dfrac{KQ}{b} = 0 &\therefore& Q_2 = \dfrac{Qa}{b} \left(\dfrac{2a}{b} -1\right) & \tiny{\blacksquare}
\end{matrix}
$• \ \text{Situação (III):}$ $\color{#3368b8}{Q_3 = \dfrac{Qa^2}{b^2} \left(3 - \dfrac{2a}{b} \right)}$\begin{matrix}
\dfrac{KQ_1}{b} + \dfrac{KQ_2}{b} + \dfrac{KQ_3}{a} = 0 &\therefore& Q_3 = \dfrac{Qa^2}{b^2} \left(3 - \dfrac{2a}{b} \right) & \tiny{\blacksquare}
\end{matrix}

