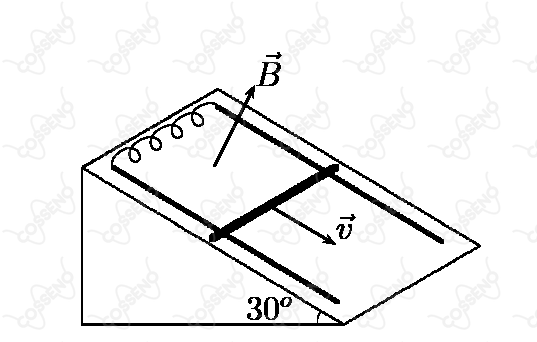
Uma haste metálica com de massa e resistência de desliza sem atrito sobre duas barras paralelas separadas de , interligadas por um condutor de resistência nula e apoiadas em um plano de com a horizontal, conforme a figura. Tudo encontra-se imerso num campo magnético , perpendicular ao plano do movimento, e as barras de apoio têm resistência e atrito desprezíveis. Considerando que após deslizar durante um certo tempo a velocidade da haste permanece constante em , assinale o valor do campo magnético.
CossenoGPT
Teste
gratuitamente agora
mesmo! 
Conforme último período do enunciado, por um certo intervalo de tempo a haste permanece com velocidade constante, ou seja, alguma força equilibra a componente do peso paralela ao plano. No caso, não é difícil dizer que essa será força a magnética, principalmente se você tiver conhecimento da $\text{lei de Lenz}$ e a $\text{lei de Faraday-Neumann}$ , isto é, o movimento da barra induz uma tensão induzida, assim como uma corrente, esta última que atribui a força magnética na direção oposta a componente do peso. Olhando apenas para a barra, temos:
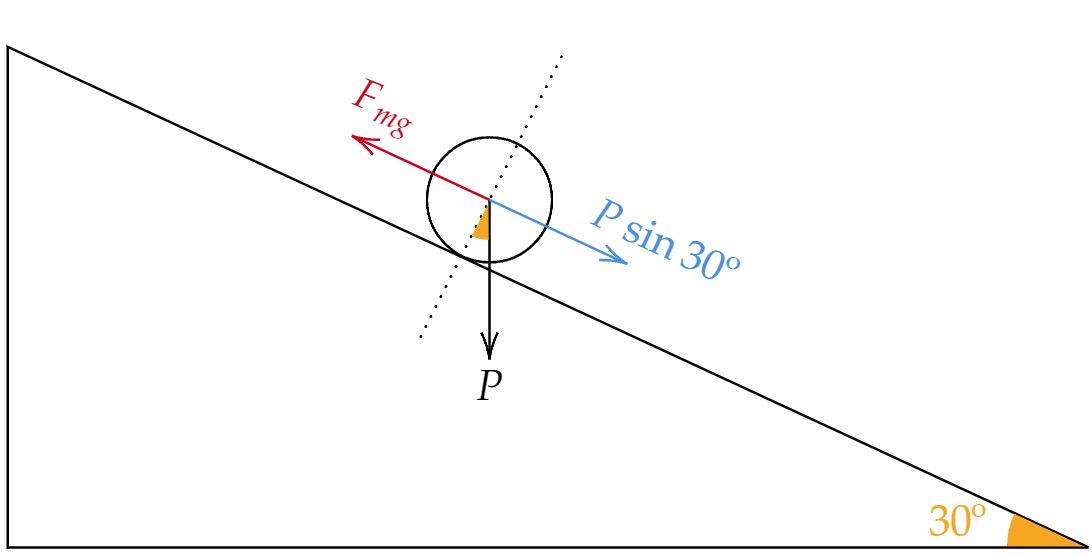No equilíbrio,\begin{align}
F_{mg} &= P \sin{30º}
\end{align}Então,\begin{matrix}Bil = mg \cdot \dfrac{1}{2} &\Rightarrow& B \cdot \dfrac{\varepsilon}{R} \cdot l = 50 \cdot \dfrac{1}{2} &\therefore& B \varepsilon = 50
\end{matrix}Com conhecimento da $\text{lei de Faraday-Neumann}$:\begin{matrix}
|\varepsilon| = \dfrac{\Phi}{\Delta t} = \dfrac{B \cdot A}{\Delta t} = B v l &\because& A = x \cdot l &,& v = \dfrac{x}{\Delta t}
\end{matrix}Portanto,\begin{matrix}
B(B v l ) = 50 &\therefore& \boxed{ B = 5 \ \pu{T}}
\end{matrix}\begin{matrix}Letra \ (E)
\end{matrix}
Ampliar Imagem
