Conforme enunciado, pode-se escrever para a reta tangente a circunferência:\begin{matrix} r_5: & y = (4q)x + 10 \end{matrix}$• \ \text{Resolução I:}$ $\color{#3368b8}{\text{Geometria}}$ Conhecida a equação da circunferência, assim como a reta em questão, é possível esboçar: 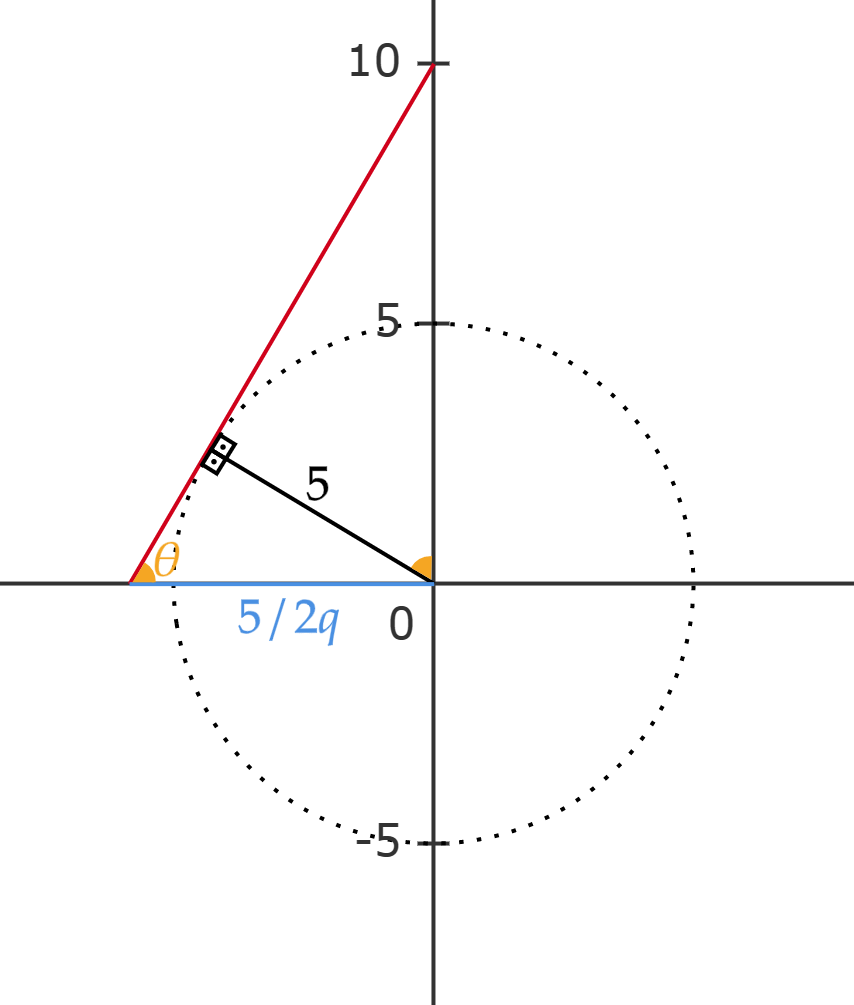Veja que $\theta$ é um ângulo notável, dado que:\begin{matrix} \cos{\theta} = \dfrac{5}{5+5} &\Rightarrow&\cos{\theta} = \dfrac{1}{2} &\therefore& \theta = 60º \end{matrix}Em posse desse resultado, segue:\begin{matrix} \sin{\theta} = \dfrac{5}{5/2q} &\Rightarrow& \dfrac{\sqrt{3}}{2} = 2q &\therefore& q = \dfrac{\sqrt{3}}{4} & \tiny{\blacksquare} \end{matrix}$• \ \text{Resolução II:}$ $\color{#3368b8}{\text{Álgebra}}$ Conhecida a equação da reta, pode-se substituir a mesma na equação da circunferência a fim de encontrar o ponto de tangência, veja:\begin{matrix} x^2 + (4qx + 10)^2 = 25 \end{matrix}Então,\begin{matrix} (16q^2 + 1)x^2 + (80q)x + 75 = 0 \end{matrix}Como se trata de um ponto de tangência, o discriminante deve ser nulo, isto é:\begin{matrix}\Delta = (80q)^2 - 4 \cdot (16q^2 + 1) \cdot 75 = 0 \end{matrix}Assim, \begin{matrix}1600q^2 = 75(16q^2 + 1) \end{matrix}Portanto,\begin{matrix} q = \dfrac{\sqrt{3}}{4} & \tiny{\blacksquare} \end{matrix}