A ideia principal é já ter a situação prévia de cabeça, isto é, conhecer a seção meridiana de uma esfera inscrita num cone. Com isso, sabemos que a partir da seção temos um grande triângulo isósceles, e um pequeno triângulo retângulo, este último devido o contado da esfera com a superfície lateral do cone, visto que o raio do cone que passa pelo ponto de contato é perpendicular a geratriz. Nesse sentido, podemos esboçar uma situação como abaixo: 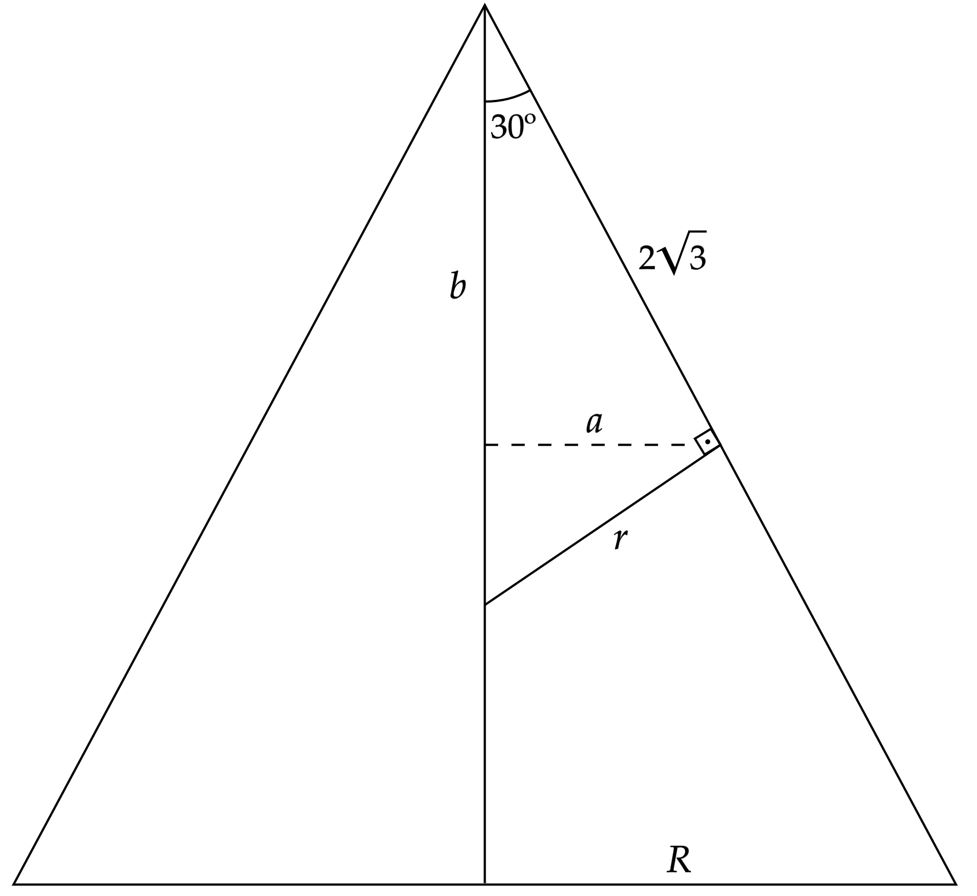$\color{#3368b8}{\text{Nota:}}$ Vale salientar que não sabemos onde está a esfera dentro do cone, quer dizer, ela pode tanto estar tocando a base do cone, quanto pode estar acima - pense numa bola dentro de uma taça. Desse modo, vamos começar encontrando $a$ e $b$, para que assim seja possível encontrar o raio $R$ da base do cone:\begin{matrix} \sin{30º} = \dfrac{a}{2\sqrt{3}} &\therefore& a = \sqrt{3} \\ \cos{30º} = \dfrac{b}{2\sqrt{3}} &\therefore& b= 3 \end{matrix}Agora, é possível encontrar o raio da base do cone por uma semelhança de triângulos, veja:\begin{matrix} \dfrac{R}{8} = \dfrac{a}{b} &\therefore& R = \dfrac{8\sqrt{3}}{3} \end{matrix}Nesse momento, resta-nos encontrar o raio da esfera, visto que a partir dele conseguiremos encontrar o volume solicitado. Assim, observe novamente a imagem anexada, trabalhando com os ângulos da figura, facilmente podemos encontrar:\begin{matrix} \sin{60º} = \dfrac{a}{r} &\therefore& r = 2 \end{matrix}Portanto, o volume $V$ requerido é apenas o volume do cone subtraído da esfera, ou seja:\begin{matrix} V = \dfrac{1}{3}\pi R^2 (8) - \dfrac{4}{3}\pi r^3 \end{matrix}Substituindo os resultados anteriores:\begin{matrix} \boxed{V = \dfrac{416}{9}\pi \ \pu{cm^3}} \end{matrix}\begin{matrix}Letra \ (A) \end{matrix}