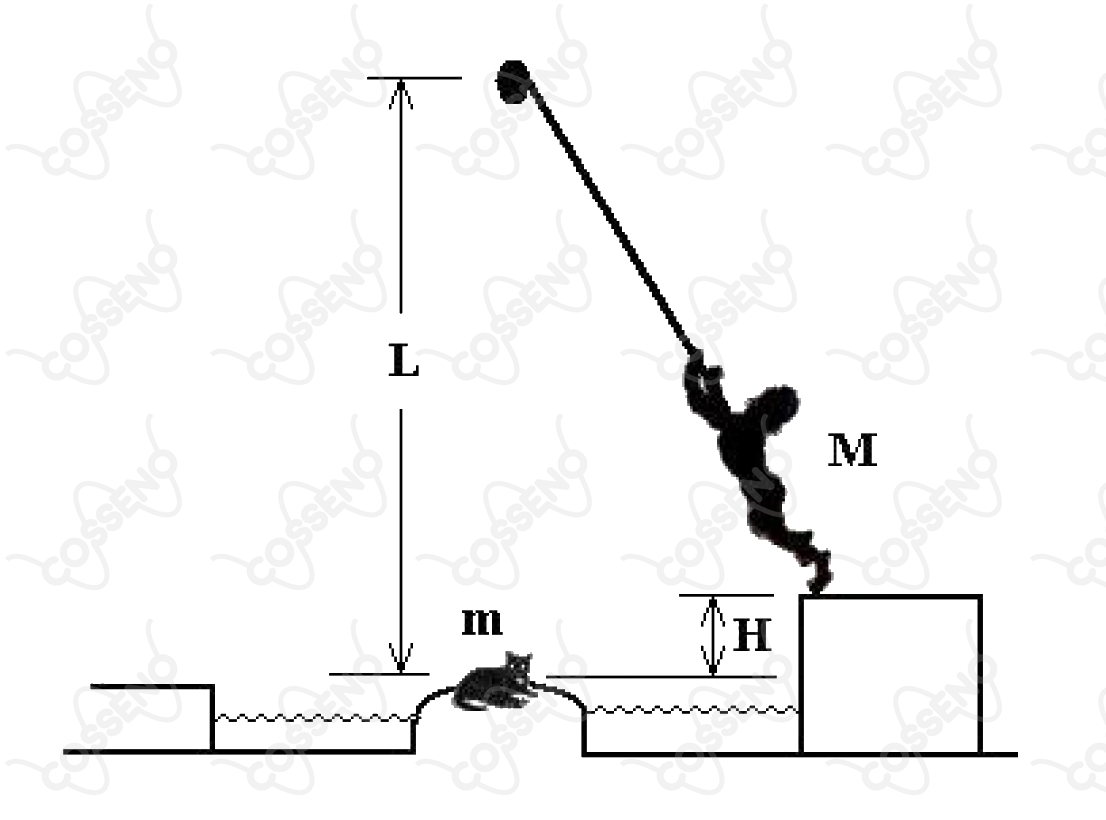
Numa brincadeira de aventura, o garoto (de massa ) lança-se por uma corda amarrada num galho de árvore num ponto de altura acima do gatinho (de massa ) da figura, que pretende resgatar.
Sendo a aceleração da gravidade e a altura da plataforma de onde se lança, indique o valor da tensão na corda, imediatamente após o garoto apanhar o gato para aterrisá-lo na outra margem do lago.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A princípio, podemos reduzir o raciocínio em três partes, encontrar a velocidade que o garoto irá chegar até o gato a partir da conservação da energia mecânica - admitimos a ausência de forças dissipativas. Adiante, fazemos a conservação do momento entre o gato e o garoto, isto é, a velocidade que o sistema gato-garoto irá adquirir quando o garoto pegar o gato. Por fim, a tração que pode ser encontrada analisando as forças que atuam no garoto, isto é, a resultante centrípeta com raio de curvatura $L$. Desse modo, vejamos:
$• \ \text{Conservação da Energia:}$ O garoto inicialmente apresenta apenas energia potencial gravitacional, esta que irá se converter em energia cinética. (Vamos admitir o nível do gato como referência).\begin{matrix}
MgH = \dfrac{Mv^2}{2} &\therefore& v^2 = 2gH
\end{matrix}$• \ \text{Conservação do Momento:}$ Não existem forças externas ao sistema, ou seja, o momento é conservado.\begin{matrix}
Mv + m0 = (m+M)u
\end{matrix}\begin{matrix} u = \dfrac{Mv}{(M+m)}
\end{matrix}$• \ \text{Tração:}$ Duas forças atuam no sistema gato-garoto, são o peso e a tração, logo, pela resultante centrípeta:\begin{matrix}
\dfrac{(M+m)u^2}{L} = T - (M+m)g
\end{matrix}\begin{matrix}
T = (M+m)g \left[ 1 + \left( \dfrac{M}{M+m}\right)^2 \dfrac{2H}{L}\right]
\end{matrix}\begin{matrix}Letra \ (D)
\end{matrix}

