No estudo de ondas que se propagam em meios elásticos, a impedância característica de um material é dada pelo produto da sua densidade pela velocidade da onda nesse material, ou seja, .
Sabe-se, também, que uma onda de amplitude , que se propaga em um meio ao penetrar em uma outra região, de meio , origina ondas, refletida e transmitida, cuja amplitudes são, respectivamente: Num fio, sob tensão , a velocidade da onda nesse meio é dada por .
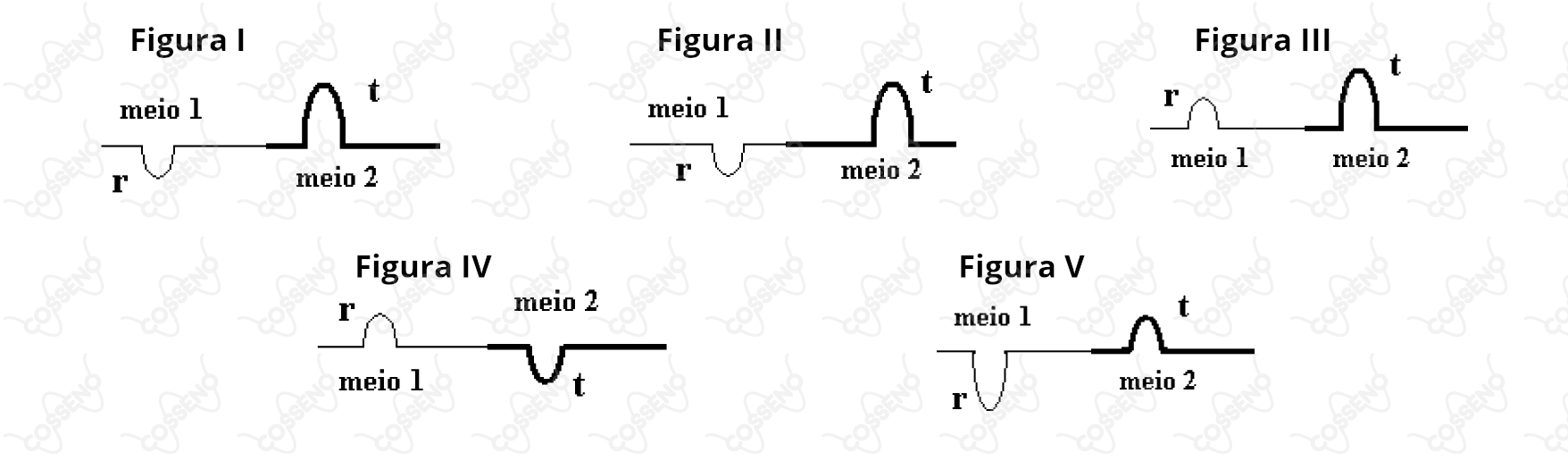
Considere agora o caso de uma onda que se propaga num fio de densidade linear (meio 1) e penetra num trecho desse fio em que a densidade linear muda para (meio ). Indique a figura que representa corretamente as ondas refletidas () e transmitida ()?
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A priori, o enunciado é bem detalhista - o que facilita a resolução - e já nos permite começar pelas impedâncias: \begin{matrix}
z_1 = \mu \sqrt{\dfrac{\tau}{\mu}} &&,&& z_2 = 4\mu \sqrt{\dfrac{\tau}{4\mu}} \\ \\
z_1 = \sqrt{\mu \tau} &&&& z_2= 2\sqrt{\mu \tau}
\end{matrix}Com posse destes resultados, vamos analisar a amplitude das ondas refletida e transmitida:\begin{matrix}
a_r = \left[ \dfrac{\dfrac{\sqrt{\mu \tau} }{2\sqrt{\mu \tau} } - 1}{\dfrac{\sqrt{\mu \tau} }{2\sqrt{\mu \tau} } + 1} \right] = - \dfrac{1}{6} \\
a_t = \left[ \dfrac{2}{1 + \dfrac{2\sqrt{\mu \tau} }{\sqrt{\mu \tau} } } \right] = +\dfrac{2}{3}
\end{matrix}Dessa forma, computamos alguns resultados, o primeiro é que as ondas estão em oposição de fase - vide sinal algébrico. Segundo, a amplitude da onda transmitida é maior que a da onda refletida, visto que: $|a_t| > |a_r|$. A par destas informações, nota-se que só há duas figuras possíveis, estão elas em $\text{I}$ e $\text{II}$. Contudo, é possível notar uma sútil diferença entre elas, na figura $\text{I}$ a onda refletida está mais distante, ou seja, ela é mais rápida que a transmitida, enquanto na figura $\text{II}$ a situação é contrária. Com isso, pela equação de Taylor fornecida no enunciado, constata-se:\begin{matrix}
v_1 = \sqrt{ \dfrac{\tau}{\mu}} &,& v_2 = \sqrt{\dfrac{\tau}{4\mu}}
\end{matrix}Portanto, a velocidade da onda no meio $2$ é menor que no meio $1$, isto é, a onda refletida é mais veloz que a transmitida.\begin{matrix}Letra \ (A)
\end{matrix}

