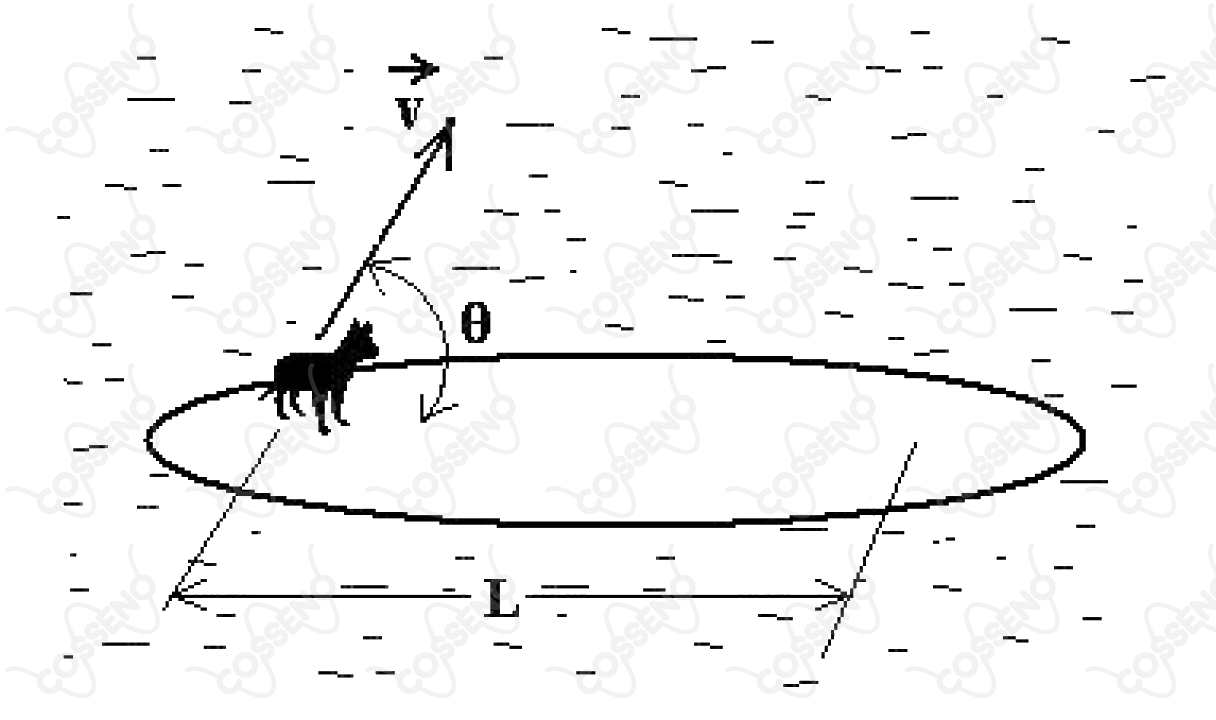
Na figura, um gato de massa encontra-se parado próximo a uma das extremidades de uma prancha de massa que flutua em repouso na superfície de um lago. A seguir, o gato salta e alcança uma nova posição na prancha, à distância . Desprezando o atrito entre a água e a prancha, sendo o ângulo entre a velocidade inicial do gato e a horizontal, e a aceleração da gravidade, indique qual deve ser a velocidade de deslocamento da prancha logo após o salto.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

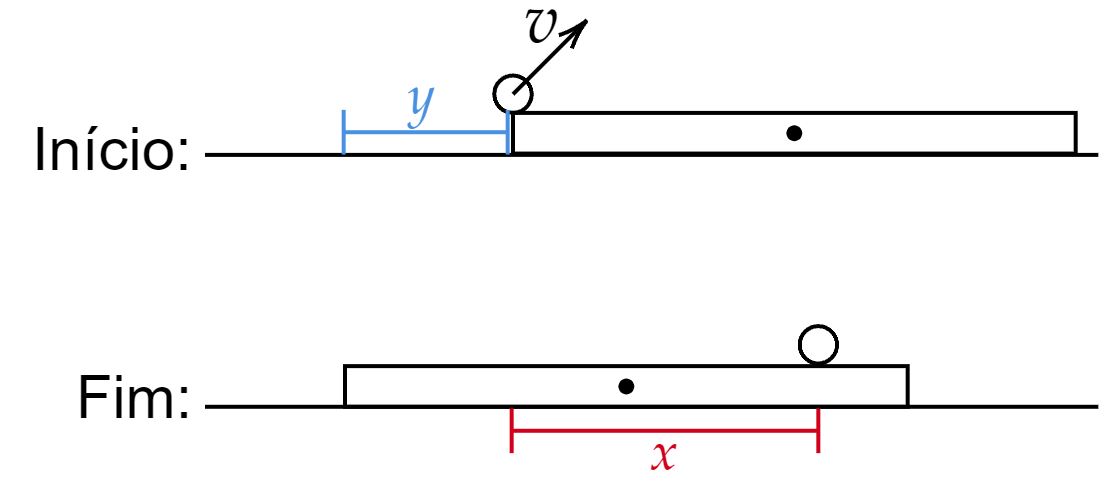
É possível começar esboçando a situação, vamos tomar a prancha como um retângulo e o gato - que inclusive parece mais um cachorro - como uma bolinha:
 Como não há forças externas agindo horizontalmente, o momento se conserva, ou seja, admitindo positivo o movimento para direita:\begin{matrix}
\Delta \vec{p} = 0 &\because& p_{inicial} = p_{final}
\end{matrix}Em que,\begin{matrix} 0 =mv_x + M(-u) &,& v_x = v\cos{\theta}
\end{matrix}\begin{matrix} \boxed{v = \dfrac{Mu}{m\cos{\theta}}} \ \ (1)
\end{matrix}Além disso, repare que a soma algébrica das distâncias $x$ e $y$ da imagem é igual a $L$, isto é:\begin{matrix} L = x + y
\end{matrix}Admitindo que tudo ocorra num intervalo de tempo $\Delta t$, podemos escrever:\begin{matrix} \dfrac{L}{\Delta t} = \dfrac{x}{\Delta t} + \dfrac{y}{\Delta t}
\end{matrix}Então,\begin{matrix} {\dfrac{L}{\Delta t} = v_x + u}
\end{matrix}Substituindo $(1)$ no resultado acima:\begin{matrix}
\boxed{\dfrac{L}{\Delta t} = u \left(\dfrac{M}{m} + 1\right)} \ \ (2)
\end{matrix}Agora, resta-nos encontrar $\Delta t$, o que não é difícil tendo conhecimento das equações horárias para o movimento vertical que o gato descreve. Nesse contexto, sabemos que o tempo de subida $t$ do gato é metade do tempo total $\Delta t$, então, admitindo o sentido para cima como positivo:\begin{matrix}
0 = v_y + (-g)t &,&v_y = v\sin{\theta} &,& \Delta t = 2t
\end{matrix}\begin{matrix}\Delta t = \dfrac{2 v\sin{\theta}}{g}
\end{matrix}Substituindo $(1)$ no resultado acima: \begin{matrix}
\Delta t = \left(\dfrac{2 Mu}{mg} \right)\tan{\theta}
\end{matrix}Por fim, comutando o resultado acima em $(2)$:\begin{matrix}
\dfrac{L}{ \left( \dfrac{2Mu}{mg}\right)\tan{\theta}} = u \left(\dfrac{M}{m} + 1\right)
\end{matrix}\begin{matrix}
\boxed{u = \sqrt{\dfrac{gLm}{ \left( 1 + \dfrac{M}{m}\right)2M\tan{\theta}} }}
\end{matrix}\begin{matrix}Letra \ (D)
\end{matrix}
Como não há forças externas agindo horizontalmente, o momento se conserva, ou seja, admitindo positivo o movimento para direita:\begin{matrix}
\Delta \vec{p} = 0 &\because& p_{inicial} = p_{final}
\end{matrix}Em que,\begin{matrix} 0 =mv_x + M(-u) &,& v_x = v\cos{\theta}
\end{matrix}\begin{matrix} \boxed{v = \dfrac{Mu}{m\cos{\theta}}} \ \ (1)
\end{matrix}Além disso, repare que a soma algébrica das distâncias $x$ e $y$ da imagem é igual a $L$, isto é:\begin{matrix} L = x + y
\end{matrix}Admitindo que tudo ocorra num intervalo de tempo $\Delta t$, podemos escrever:\begin{matrix} \dfrac{L}{\Delta t} = \dfrac{x}{\Delta t} + \dfrac{y}{\Delta t}
\end{matrix}Então,\begin{matrix} {\dfrac{L}{\Delta t} = v_x + u}
\end{matrix}Substituindo $(1)$ no resultado acima:\begin{matrix}
\boxed{\dfrac{L}{\Delta t} = u \left(\dfrac{M}{m} + 1\right)} \ \ (2)
\end{matrix}Agora, resta-nos encontrar $\Delta t$, o que não é difícil tendo conhecimento das equações horárias para o movimento vertical que o gato descreve. Nesse contexto, sabemos que o tempo de subida $t$ do gato é metade do tempo total $\Delta t$, então, admitindo o sentido para cima como positivo:\begin{matrix}
0 = v_y + (-g)t &,&v_y = v\sin{\theta} &,& \Delta t = 2t
\end{matrix}\begin{matrix}\Delta t = \dfrac{2 v\sin{\theta}}{g}
\end{matrix}Substituindo $(1)$ no resultado acima: \begin{matrix}
\Delta t = \left(\dfrac{2 Mu}{mg} \right)\tan{\theta}
\end{matrix}Por fim, comutando o resultado acima em $(2)$:\begin{matrix}
\dfrac{L}{ \left( \dfrac{2Mu}{mg}\right)\tan{\theta}} = u \left(\dfrac{M}{m} + 1\right)
\end{matrix}\begin{matrix}
\boxed{u = \sqrt{\dfrac{gLm}{ \left( 1 + \dfrac{M}{m}\right)2M\tan{\theta}} }}
\end{matrix}\begin{matrix}Letra \ (D)
\end{matrix}

Ampliar Imagem

