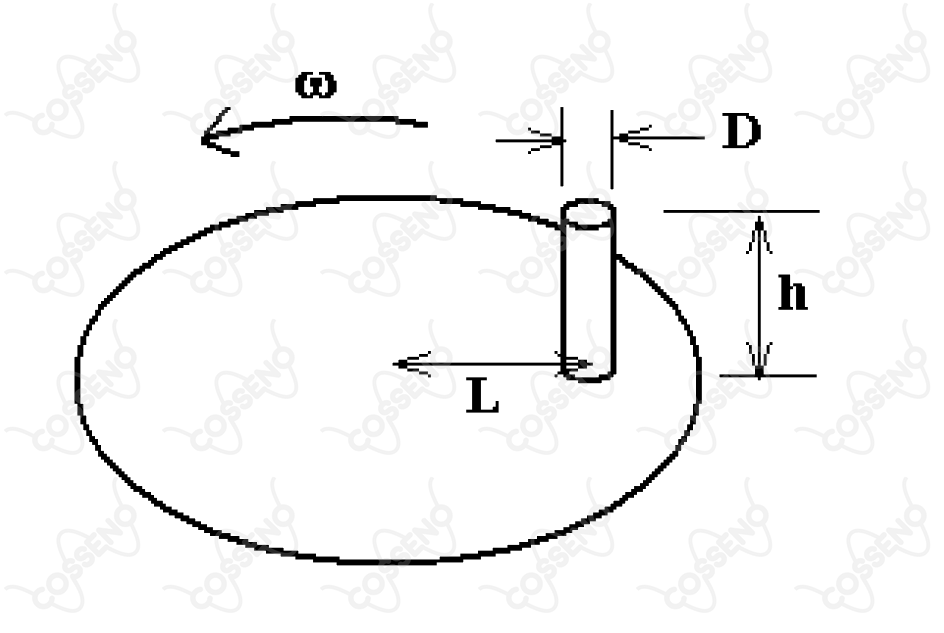
Um cilindro de diâmetro e altura repousa sobre um disco que gira num plano horizontal, com velocidade angular . Considere o coeficiente de atrito entre o disco e o cilindro a distância entre o eixo do disco e o eixo do cilindro, e a aceleração da gravidade. O cilindro pode escapar do movimento circular de duas maneiras: por tombamento ou por deslizamento.
Mostrar o que ocorrerá primeiro, em função das variáveis.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Na situação da figura, a força de atrito atua como resultante centrípeta, logo
$$f_{at} = m \omega_{1}^{2}L \Rightarrow \mu mg \leq m \omega_{1}^{2}L \Rightarrow \omega_{1_{máx}} = \sqrt{\dfrac{\mu g}{L}}.$$
Equilibrando os torques em relação ao centro de massa do corpo.
$$m \omega_{2}^{2}L \cdot \dfrac{h}{2} \leq mg\dfrac{D}{2} \Rightarrow \omega_{2_{máx}} = \sqrt{\dfrac{gD}{Lh}}.$$
Logo, $\omega_{1_{máx}} > \omega_{2_{máx}}$, então haverá tombamento antes de escorregar.
Extra: Para aprender mais sobre tombamento, recomendo "Estática V - Tombamento x Escorregamento" do Virando Olímpico.

