Para resolver a questão de forma rápida, é valioso conhecer o comportamento da função quadrática, do logaritmo e do módulo. É interessante esboçar a função quadrática: 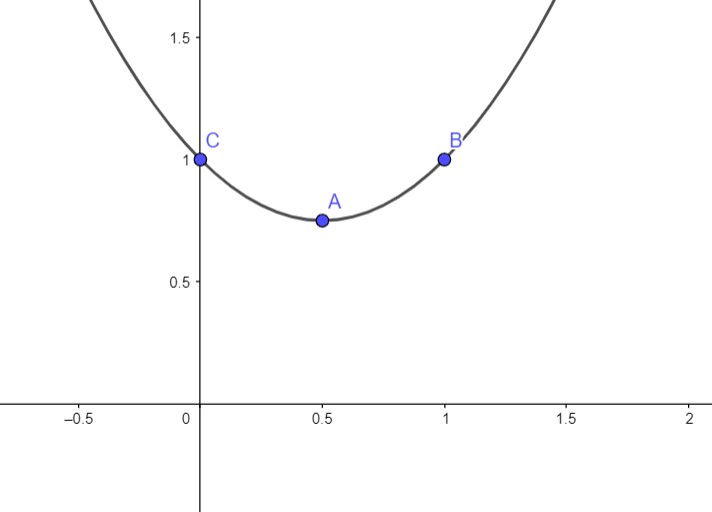A função $$y = x^2 - x + 1$$ possui como ponto de mínimo $A = (\frac{1}{2}, \frac{3}{4})$. Isso significa que para cada $x_0$ à direita de $x_{vértice} = 0,5$ existe um $x_1$ simétrico para esquerda tal que $y(x_0) = y(x_1)$. De posse dessa observação, podemos descartar os itens $A, B$ e $D$. Caso não houvesse o módulo aplicado, os itens $C$ e $E$ estariam corretos. Todavia, para $0 < x < 1$, $\ln {x} < 0$ e portanto seu módulo assume valores que podem ser obtidos com $x > 1$ também. Tal fato descarta o item $E$. Logo a resposta é a $Letra \ C$