Pensando em driblar o trabalho algébrico, assim como analisando os dados do enunciado, uma forma direta seria tentar resolver a questão por análise geométrica. Nesse sentido, vamos esboçar como o problema ficaria no plano de Argand-Gauss: 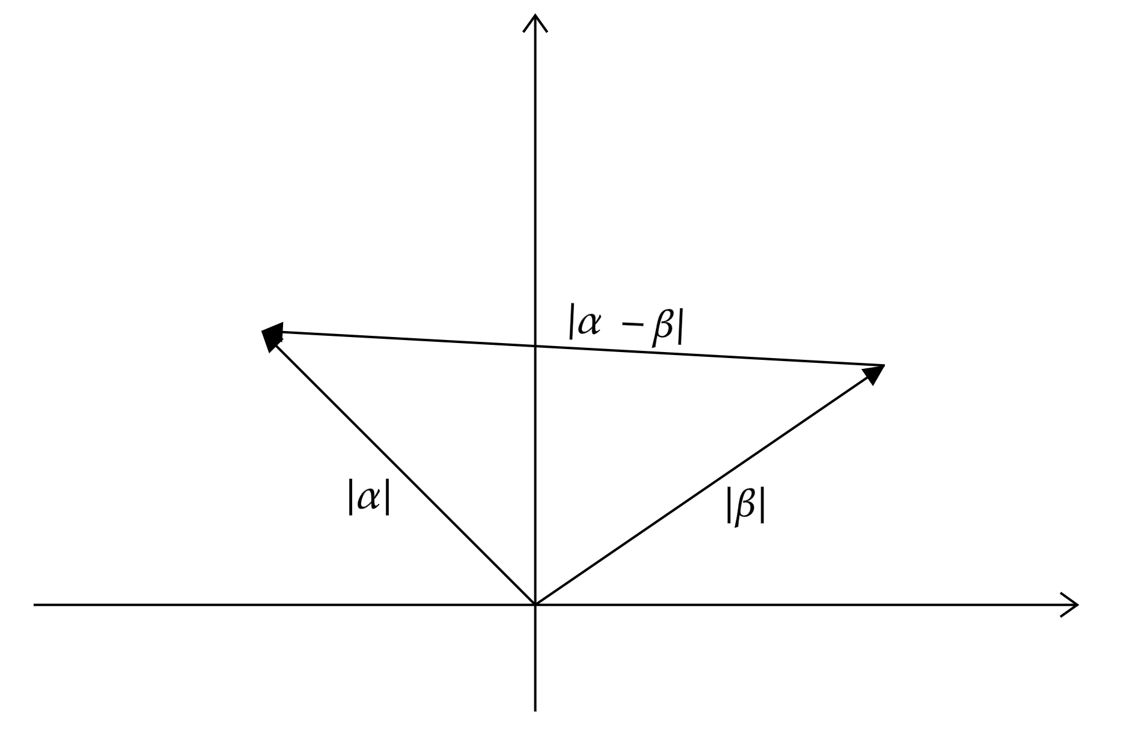Não é difícil perceber que o triângulo é retângulo, visto que, conforme teorema de Pitágoras:\begin{matrix} |\alpha - \beta|^2 = |\alpha|^2 + |\beta|^2 \end{matrix}$\color{orangered}{\text{Obs:}}$ Você também poderia verificar isso simplesmente analisando a forma polar de $\alpha - \beta$. Com isso, pensando nos argumentos de $\alpha$ e $\beta$, devemos ter:\begin{matrix} \hat{\alpha} - \hat{\beta} = 90º \end{matrix}Agora, para a forma polar dos complexos em questão, podemos escrever:\begin{matrix} \alpha = |\alpha|\cdot [\cos{(\hat{\alpha})} + i\sin{(\hat{\alpha})}] \\ \beta= |\beta|\cdot [\cos{(\hat{\beta})} + i\sin{(\hat{\beta})}] \end{matrix}Então,\begin{matrix} \beta= \cos{(\hat{\alpha} - 90º)} + i\sin{(\hat{\alpha} - 90º)} \\ \beta = \sin{(\hat{\alpha})} - i\cos{(\hat{\alpha})} \end{matrix}Multiplicando a equação por $i$, nota-se:\begin{matrix} i\beta =\cos{(\hat{\alpha})} + i\sin{(\hat{\alpha})} \\ i\beta = \alpha \\ \boxed{\alpha^2 + \beta^2 = 0} \end{matrix}\begin{matrix}Letra \ (B) \end{matrix}$\color{#3368b8}{\text{Resolução alternativa:}}$\begin{matrix} \alpha - \beta = |\alpha - \beta|\cdot [\cos{(\hat{\alpha} -\hat{ \beta})} + i\sin{(\hat{\alpha} - \hat{\beta})}] \end{matrix}\begin{matrix}\alpha - \beta = \sqrt{2} \end{matrix}Ou seja,\begin{matrix} \cos{(\hat{\alpha})} - \cos{(\hat{\beta})} + i[\sin{(\hat{\alpha})} - \sin{(\hat{\beta})}] = \sqrt{2} \end{matrix}Então,\begin{matrix} \cos{(\hat{\alpha})} - \cos{(\hat{\beta})} &=& \sqrt{2} \\ \sin{(\hat{\alpha})} - \sin{(\hat{\beta})} &=& 0 \end{matrix}Existem diversas formas de trabalhar o resultado acima, porém, creio que a mais simples seja fazer: \begin{matrix} \hat{\alpha} + \hat{\beta} = 180º \\ \hat{\alpha} = 135º \ \ \wedge \ \ \hat{\beta} = 45º \end{matrix}Em que,\begin{matrix} \alpha^2 + \beta^2 = [\cos{(2\hat{\alpha})} + i\sin{(2\hat{\alpha})}] + [\cos{(2\hat{\beta})} + i\sin{(2\hat{\beta})}] \\ \boxed{\alpha^2 + \beta^2 = 0} \end{matrix}

Se pensarmos nos arcos notáveis, os quais sendo argumentos de números complexos cujos módulos são iguais a 1, podemos pensar em alguns argumentos até chegar num resultado que satisfaça o enunciado. Isto é um trabalho mental muito importante em momentos de provas, a fim de fugir de algebrismos e muitas operações desnecessárias. Se $\alpha = \large{\frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2} i}$ e $\beta = \large{- \frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2} i}$ $\implies$ $|\alpha| = |\beta| = 1$ e $|\alpha - \beta| = \sqrt 2$ . Coloquemos nas formas trigonométricas: $\alpha = cis(\frac{\pi}{4})$ e $\beta = -\space cis(- \frac{\pi}{4})$ . Portanto: $\alpha^2 + \beta^2$ $=$ $cis^2(\frac{\pi}{4}) + [-cis(- \frac{\pi}{4}) ]^2$ $=$ $cis(\frac{\pi}{2}) + cis(- \frac{\pi}{2})$ $\boxed{\alpha^2 + \beta^2 = i - i = 0}$