Considere o quadrado com lados de 10m de comprimento. Seja M um ponto sobre o lado e um ponto sobre o lado ; eqüidistantes de . Por M traça-se uma reta r paralela ao lado e por uma reta s paralela ao lado ; que se interceptam no ponto . Considere os quadrados AMON e OPCQ, onde é a intersecção de s com o lado e é a intersecção de r com o lado . Sabendo- se que as áreas dos quadrados e constituem, nesta ordem, uma progressão geométrica, então a distância entre os pontos e é igual, em metros, a
CossenoGPT
Teste
gratuitamente agora
mesmo! 
Esboçando a situação conforme enunciado:
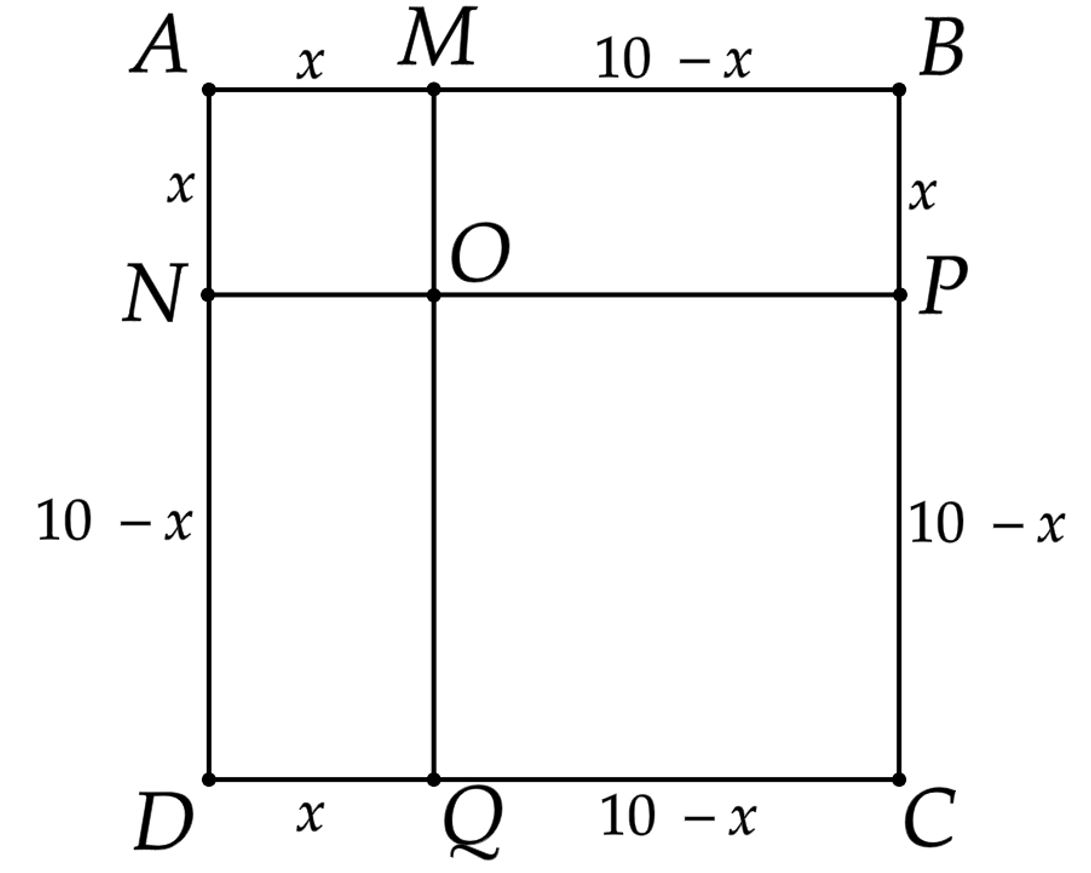Conforme progressão geométrica, deve-se ter:\begin{matrix}
\ce{[OPCQ] = \sqrt{[AMON] \cdot [ABCD] }}
\end{matrix}Como todas as figuras são retângulos, temos simplesmente:\begin{matrix}
(10-x)^2 = 10x
\end{matrix}\begin{matrix}x^2 -30x + 100 = 0
\end{matrix}\begin{matrix}x = \dfrac{30 \pm 10\sqrt{5}}{2}
\end{matrix}Observe que a raiz positiva não satisfaz o problema, visto que $x<10$, portanto:\begin{matrix} \boxed{x = 15 - 5\sqrt{5}}
\end{matrix}\begin{matrix}Letra \ (D)
\end{matrix}
Ampliar Imagem
