Veja a figura abaixo. 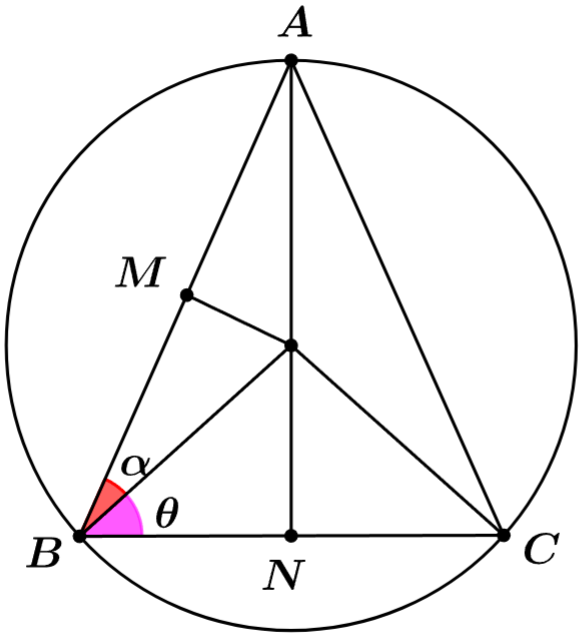No desenho foi traçado segmentos de reta que ligam os vértices do triângulo acutângulo até o centro da circunferência. Além disso, perceba outros dois segmentos de reta que ligam o centro da circunferência até os pontos $M$ e $N$ destacados na figura, esses pontos dividem os segmentos $AB$ e $BC$ ao meio (ponto médio). Por que isso foi feito? Porque teremos dois triângulos retângulos e iremos conseguir encontrar o seno do ângulo $A\hat{B}C$. \begin{align} [ABC] = \dfrac{\overline{AB} \cdot \overline{BC} \cdot \sin (\alpha + \theta)}{2} \\ \sin (\alpha + \theta) = \sin \alpha cos \theta + \sin \theta \cos \alpha \end{align} Pelo teorema de Pitágoras: $$(\sqrt{5})^{2} + x^{2} = \left(\dfrac{5\sqrt{2}}{2}\right)^{2} \Rightarrow x = \dfrac{\sqrt{5}}{3}\\ (\sqrt{2})^{2} + y^{2} = \left(\dfrac{5\sqrt{2}}{2}\right)^{2} \Rightarrow y = \dfrac{4\sqrt{2}}{3}$$ Aplicando definição de seno e cosseno. \begin{align} \sin (\alpha) = \dfrac{\left(\dfrac{\sqrt{5}}{3}\right)}{\left(\dfrac{5\sqrt{2}}{3}\right)} = \dfrac{\sqrt{5}}{5\sqrt{2}} \\ \cos (\alpha) = \dfrac{\sqrt{5}}{\left(\dfrac{5\sqrt{2}}{3}\right)} = \dfrac{3\sqrt{5}}{5\sqrt{2}} \\ \sin(\theta) = \dfrac{\left(\dfrac{4\sqrt{2}}{3}\right)}{\left(\dfrac{5\sqrt{2}}{3}\right)} = \dfrac{4}{5} \\ \cos(\theta) = \dfrac{\sqrt{2}}{\left(\dfrac{5\sqrt{2}}{3}\right)} = \dfrac{3}{5} \end{align} Substituindo $(3), (4), (5)$ e $(6)$ em $(2)$ e com o resultado de $(2)$, substituir em $(1)$, temos que $$[ABC] = 6 \ ua$$