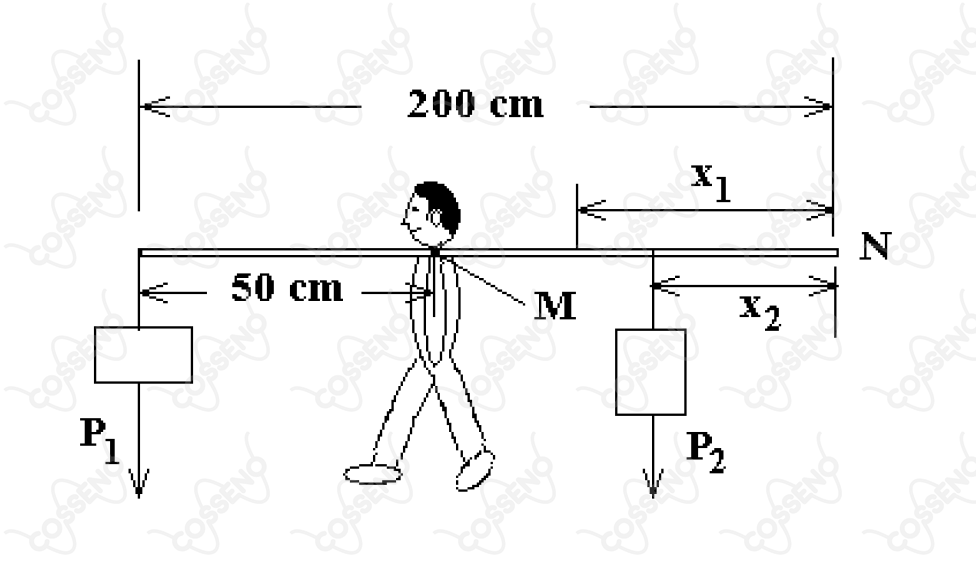
Na experiência idealizada na figura, um halterofilista sustenta, pelo ponto , um conjunto em equilíbrio estático composto de uma barra rígida e uniforme, de um peso na extremidade a de , e de um peso , na posição indicada.
A seguir, o mesmo equilíbrio estático é verificado dispondo-se, agora, o peso na posição original de , passando este à posição de distância da extremidade . Sendo de o comprimento da barra e a aceleração da gravidade, a massa da barra é de
CossenoGPT
Teste
gratuitamente agora
mesmo! 
$\text{Situação inicial:}$
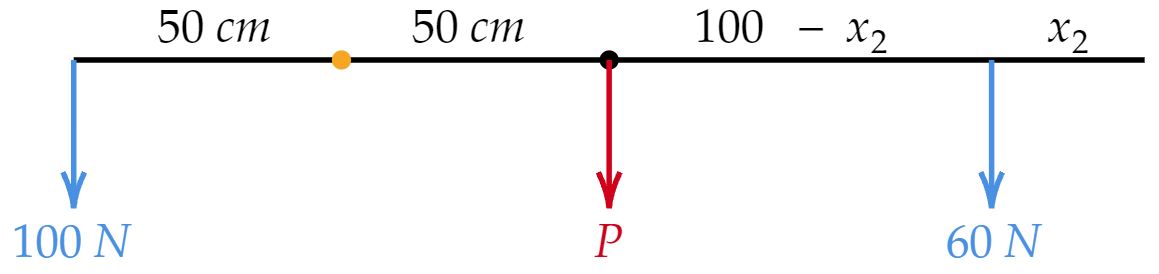Analisando o momento das forças em relação ao ponto de sustentação:\begin{matrix}
100 \cdot 50 = 50 \cdot P + (150-x_2) \cdot 60 \\
\boxed{6x_2= 5P + 400 \ \ (1)}
\end{matrix}$\text{Situação final:}$
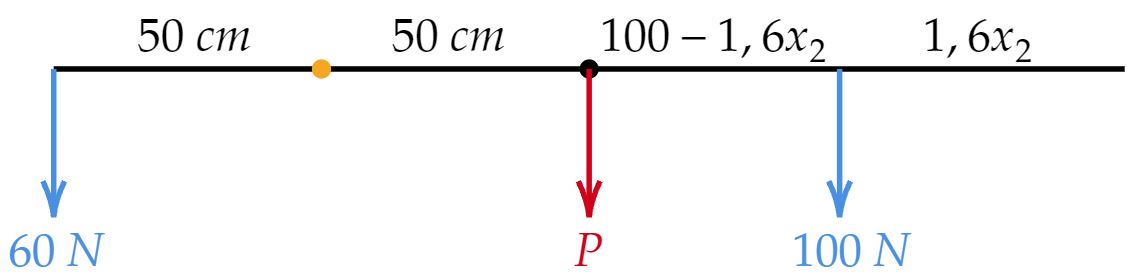Analogamente,\begin{matrix}
60\cdot 50 = 50 \cdot P + (150-1,6x_2) \cdot 100 \\
\boxed{16x_2= 5P + 1200\ \ (2)}
\end{matrix}Subtraindo $(1)$ de $(2)$, têm-se:\begin{matrix}
10x_2 = 1200 - 400 \\ \boxed{x_2 = 80 \ \pu{cm}}
\end{matrix}Substituindo o resultado acima em qualquer uma das equações anteriores, constata-se:\begin{matrix}
5P = 80 &,& P =10m
\end{matrix}\begin{matrix}\boxed{m = 1,6 \ \pu{kg}}
\end{matrix}\begin{matrix}Letra \ (D)
\end{matrix}
Ampliar Imagem
Ampliar Imagem
