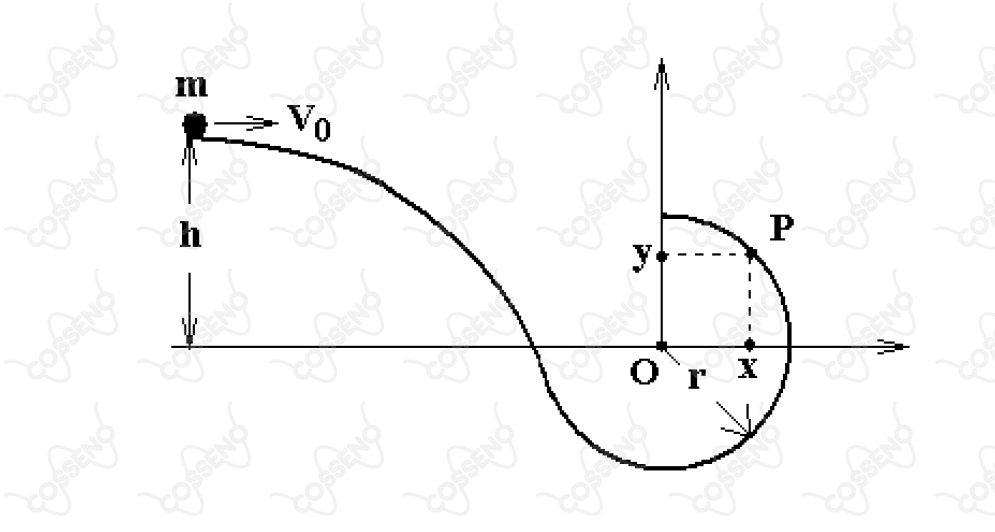
Um corpo de massa e velocidade a uma altura desliza sem atrito sobre uma pista que termina em forma de semi-circunferência de raio , conforme indicado na figura. Determine a razão entre as coordenadas e do ponto na semi-circunferência, onde o corpo perde o contato com a pista. Considere a aceleração da gravidade .
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Por conservação de energia:
$$mg(h+r) + \dfrac{mv_{0}^{2}}{2} = mg(r+y) + \dfrac{mv^{2}}{2} \ \Leftrightarrow \ g(h-y) + \dfrac{v_{0}^{2}}{2} = \dfrac{v^{2}}{2}.$$
Nossa missão agora é encontrar o valor da velocidade no ponto indicado na figura, em que o corpo perde o contato com a pista, isto é, a normal é igual a zero.
$$\dfrac{mv^{2}}{r} = mg\cos \theta \ \Leftrightarrow \ \dfrac{v^{2}}{2} = \dfrac{gr\cos \theta}{2}.$$
Pela geometria do problema, podemos facilmente encontrar uma relação para o cosseno de $\theta$. Sabe-se que
$$\cos \theta = \dfrac{y}{r},$$
com isso, obtemos que
$$y = \dfrac{2gh + v_{0}^{2}}{3g}.$$
Aplicando o teorema de Pitágoras, em que $x^{2} + y^{2} = r^{2}$. Com isso, basta dividir ambos os lados por $y^{2}$ e isolar a razão $\frac{x}{y}$ e iremos obter que
$$\dfrac{x}{y} = \sqrt{\dfrac{9g^{2}r^{2}}{(v_{0}^{2} + 2gh)^{2}} - 1}.$$

