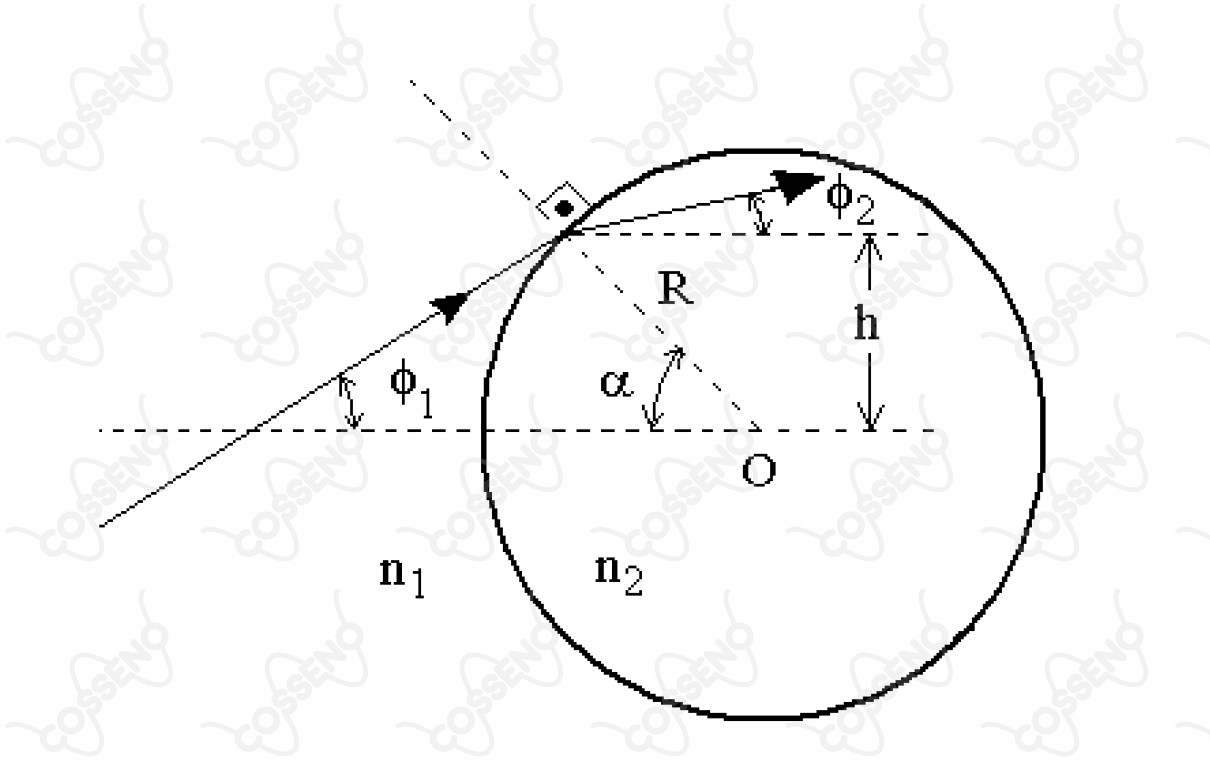
A figura mostra um raio de luz propagando-se num meio de índice de refração e transmitido para uma esfera transparente de raio e índice de refração . Considere os valores dos ângulos e muito pequenos, tal que cada ângulo seja respectivamente igual à sua tangente e ao seu seno. O valor aproximado de é de
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Pensando na $\text{Lei de Snell}$:\begin{matrix}
\dfrac{\sin{(\alpha + \phi_2)}}{\sin{(90º)}} = \dfrac{n_1}{n_2}
\end{matrix}$\color{orangered}{\text{Obs:}}$ Repare nos ângulos alternos internos, mais precisamente em $\alpha$.
Analisando a geometria do problema, pode-se perceber:\begin{matrix}
\alpha + \phi_1+ 90º = 180º \\
\boxed{\alpha + \phi_1 = 90º}
\end{matrix}Com isso, pela lei de Snell:\begin{matrix}
\dfrac{\sin{(\alpha + \phi_2)}}{\sin{(\alpha + \phi_1 )}} = \dfrac{n_1}{n_2}
\end{matrix}Segundo o enunciado, o seno do ângulo é aproximadamente o próprio ângulo, logo:\begin{matrix}\dfrac{{(\alpha + \phi_2)}}{{(\alpha + \phi_1 )}} = \dfrac{n_1}{n_2} \\
\boxed{\phi_2 = \dfrac{n_1}{n_2}\phi_1 + \left( \dfrac{n_1}{n_2} -1\right)\alpha} \\ \\ Letra \ (E)
\end{matrix}

