Veja a figura a seguir: 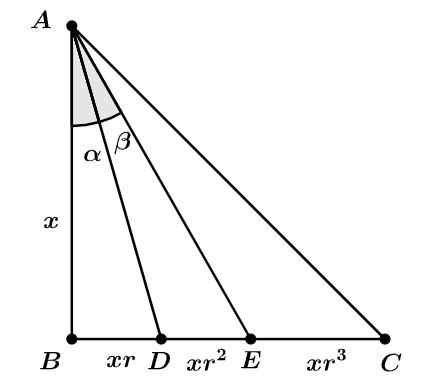Nela é possível visualizar a situação proposta pelo problema. Para começar, é mais fácil calcular a tangente do ângulo $\alpha$ e depois usar a tangente da soma dos arcos $\alpha$ e $\beta$ para tentar isolar a tangente de $\beta$. $$\tan \alpha = \dfrac{xr}{x} = r \ (I)$$ $$\tan (\alpha + \beta) = \dfrac{r + \tan \beta}{1 - r\tan \beta} = \dfrac{x(r+r^{2})}{x} = r+r^{2} \Rightarrow r + \tan \beta = (r + r^{2})(1 - r\tan \beta) \Rightarrow \\ \Rightarrow \tan \beta = \dfrac{r^{2}}{r^{3} + r^{2} + 1} \ (II).$$ Lembrando que o enunciado nos informou a respeito dos lado em progressão geométrica, então $$x = xr + xr^{2} + xr^{3} \Rightarrow = r^{3} + r^{2} = 1 - r.$$ Logo, $$\tan \beta = \dfrac{r^{2}}{2 - r}.$$