Animado com velocidade inicial , o objeto , de massa , desliza sobre um piso horizontal ao longo de uma distância , ao fim da qual colide com o objeto , de mesma massa, que se encontra inicialmente parado na beira de uma escada de altura . Com o choque, o objeto atinge o solo no ponto . Chamando o coeficiente de atrito cinético entre o objeto e o piso, a aceleração da gravidade e desprezando a resistência do ar, assinale a expressão que dá a distância .
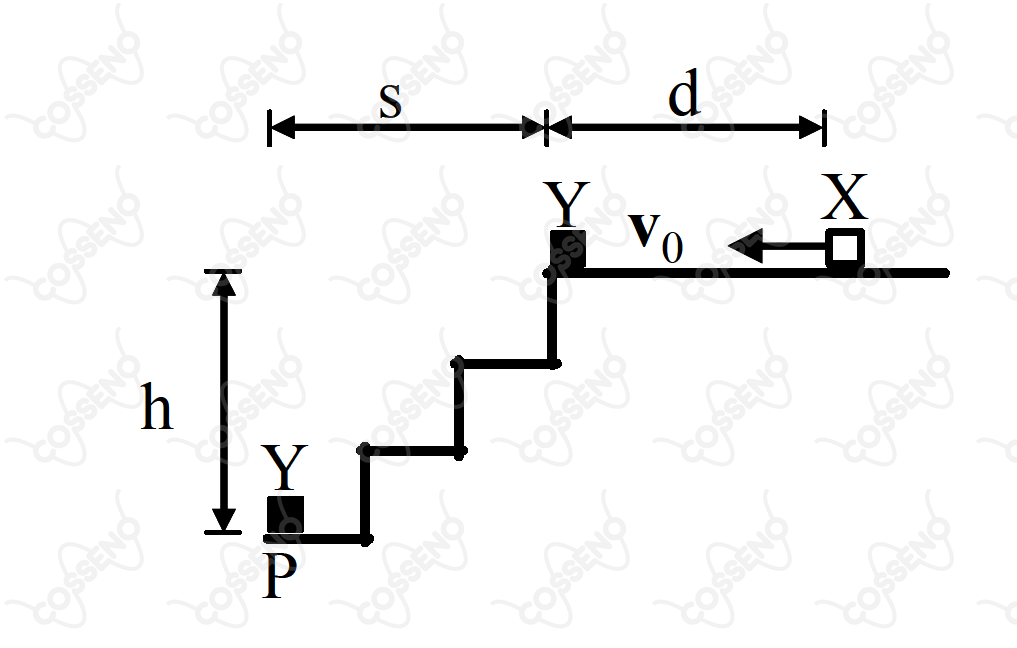
Admita colisão elástica
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A princípio, podemos pensar no $\text{Teorema da Energia Cinética}$ a fim de encontrar a velocidade $v$ que o objeto $X$ atinge o $Y$. Nesse sentido, têm-se:\begin{matrix}W_T = \Delta E_c &\Rightarrow&
-F_{atrito} \cdot d = \dfrac{mv^2}{2} - \dfrac{mv_0^2}{2} &\therefore&
d = \dfrac{1}{2g\mu_k}\left( v_0^2 - v^2\right) \ \ \text{(I)}
\end{matrix}Com isso, resta-nos encontrar a velocidade $v$, para isso, veja que a colisão é perfeitamente elástica entre dois corpos de mesma massa, ou seja, a velocidade que $Y$ adquire é justamente $v$. Adiante, nota-se um lançamento horizontal de $Y$, analisando o movimento em cada eixo, podemos escrever:\begin{matrix}
\text{Eixo Horizontal (MRU):} & S = v \cdot \Delta t \\
\text{Eixo Vertical (MRUV):} & h = \dfrac{g \cdot (\Delta t)^2}{2}
\end{matrix}Isolando o tempo em qualquer uma das equações e substituindo na outra, contata-se:\begin{matrix}v = S\sqrt{\dfrac{g}{2h}}
\end{matrix}Substituindo o resultado acima em $\text{(I)}$:\begin{matrix}
\boxed{d = \dfrac{1}{2g\mu_k}\left( v_0^2 - \dfrac{S^2g}{2h}\right) } \\ \\ Letra \ (A)
\end{matrix}

