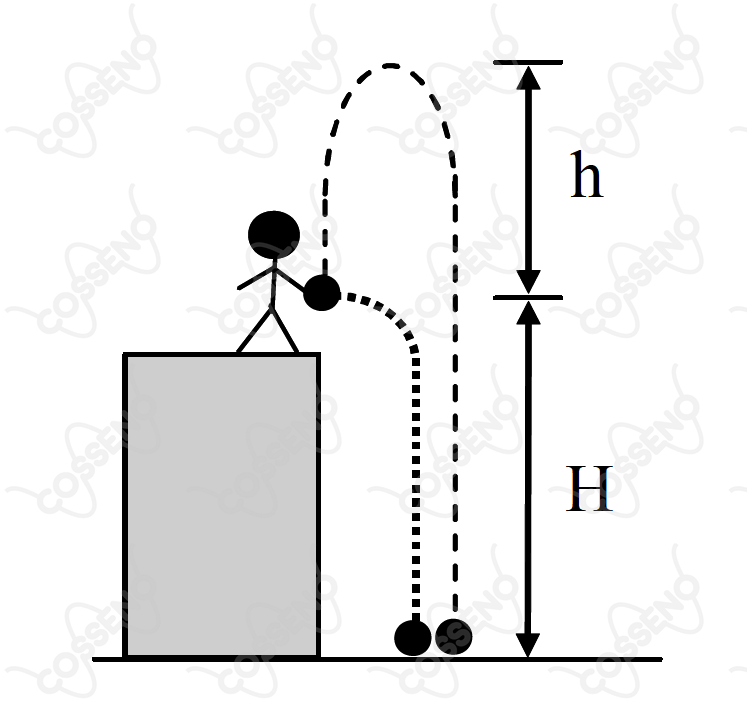
À borda de um precipício de um certo planeta, no qual se pode desprezar a resistência do ar, um astronauta mede o tempo que uma pedra leva para atingir o solo, após deixada cair de uma de altura . A seguir, ele mede o tempo que uma pedra também leva para atingir o solo, após ser lançada para cima até uma altura , como mostra a figura. Assinale a expressão que dá a altura .
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Admitindo que a gravidade do planeta seja $a$, vamos começar encontrando o período de tempo $t_1$, e isolando $a$, visto que ele não consta nas alternativas:\begin{matrix}
H = \dfrac{a(t_1)^2}{2} &\Rightarrow& a = \dfrac{2H}{(t_1)^2}
\end{matrix}Pensando na segunda situação, façamos em dois tempos, o de subida $t_s$, e o de descida $t_d$, a soma algébrica dos dois deve resultar em $t_2$, assim:\begin{matrix}
h = \dfrac{a(t_s)^2}{2} &,& H + h = \dfrac{a(t_d)^2}{2}
\end{matrix}Com isso,\begin{matrix} t_s + t_d = \sqrt{\dfrac{2h}{a}} + \sqrt{\dfrac{2(H+ h)}{a}} = t_2
\end{matrix}Substituindo o $a$ que anteriormente isolamos:\begin{matrix}
\sqrt{\dfrac{(t_1)^2h}{H}} + \sqrt{\dfrac{(t_1)^2(H+ h)}{H}} = t_2
\end{matrix}A partir daqui o trabalho é puramente algébrico, logo:\begin{matrix}
\sqrt{\dfrac{h}{H}} + \sqrt{\dfrac{(H+ h)}{H}} = \dfrac{t_2}{t_1} \\ \\
\left ( \sqrt{\dfrac{H+ h}{H}} \right)^2 = \left ( \dfrac{t_2}{t_1} - \sqrt{\dfrac{h}{H}} \right)^2 \\ \\
1 + \dfrac{h}{H} = \left ( {\dfrac{t_2}{t_1}} \right)^2 + \dfrac{h}{H} -2\dfrac{t_2}{t_1}\sqrt{\dfrac{h}{H}} \\ \\
2\dfrac{t_2}{t_1}\sqrt{\dfrac{h}{H}} = \left ( {\dfrac{t_2}{t_1}} \right)^2 - 1 \\ \\
2t_2\sqrt{\dfrac{h}{H}} = \dfrac{t_2^2 - t_1^2}{t_1} \\ \\ \boxed{H = \dfrac{4t_1^2 t_2^2}{(t_2^2 - t_1^2)^2}}
\end{matrix}\begin{matrix}Letra \ (E)
\end{matrix}

19:43 16/09/2023
O tempo de subida é o mesmo tempo que levaria para largar a bola de uma dada altura. Imaginando essa situação de largar a bola de uma certa altura, com a equação geral do movimento, temos o resultado notável que $$t_s = \sqrt{\frac{2h}{g}}$$ Assim, a velocidade inicial não é requerida para encontrar o tempo de subida, uma vez que temos a altura h e a aceleração da gravidade g.

19:44 16/09/2023
O LaTeX não apareceu, mas é só colocar no bloco de resolução aqui embaixo.

19:25 14/09/2023
Pq no tempo de subida não apareceu a velocidade com que ele lança a bolinha?

