A priori, vamos pensar num hexágono regular inscrito numa circunferência, assim como uma circunferência inscrita num hexágono regular- de modo sequencial: 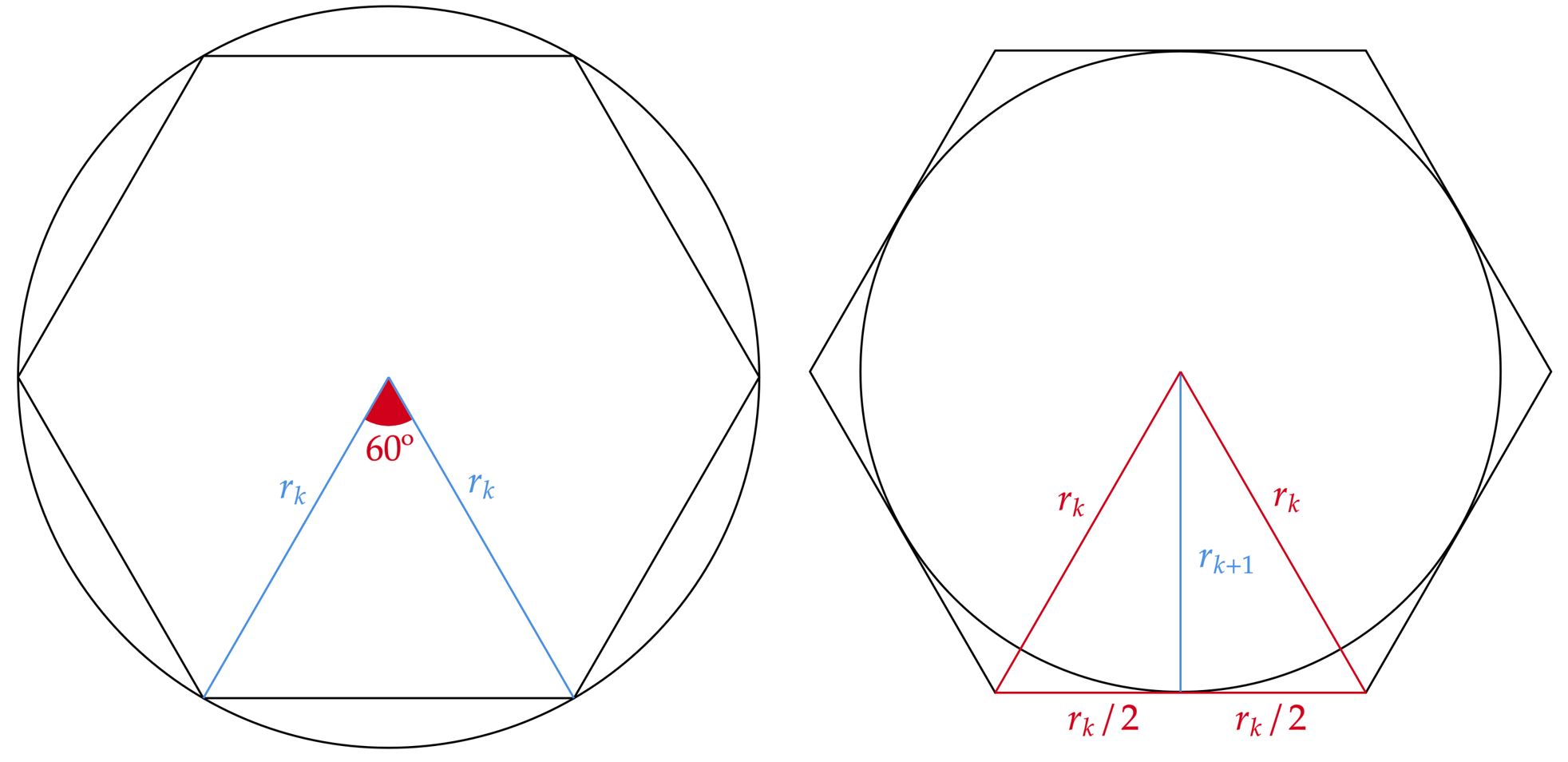Observe que calcular a área de um hexágono regular inscrito é relativamente fácil, pois ele é composto por seis triângulos equiláteros de lados iguais ao raio da circunferência circunscrita. Nessa perspectiva, podemos escrever e generalizar:\begin{matrix} A_k = 6 \cdot \left[ \dfrac{(r_k)^2\sqrt{3}}{4}\right] = \dfrac{3}{2}(r_k)^2\sqrt{3} \end{matrix}Por outro lado, também podemos encontrar a área do hexágono pela circunferência inscrita de forma análoga:\begin{matrix} A_k = 6 \cdot \left( \dfrac{r_{k+1} \cdot r_k}{2}\right) = 3(r_{k+1} \cdot r_k) \end{matrix}Igualando os resutados:\begin{matrix} 3(r_{k+1} \cdot r_k) = \dfrac{3}{2}(r_k)^2\sqrt{3} &\therefore& r_k = \dfrac{2\sqrt{3}}{3} r_{k+1} \end{matrix}Pondere que isso nos garante uma progressão geométrica, utilizando do nosso primeiro resultado, consegue-se evidenciar mais ainda:\begin{matrix} \dfrac{A_{k+1}}{A_{k}} =\left( \dfrac{ r_{k+1}}{r_{k}}\right)^2 = \dfrac{3}{4} \end{matrix}Desse modo, nota-se que o somatório solicitado nada mais é que a soma duma progressão geométrica infinita de razão $3/4$. Portanto, verifica-se:\begin{matrix} \overset{\infty}{\underset{n=1}{\sum}} A_n = \dfrac{A_1}{1 - \dfrac{3}{4}} = 4 \cdot \left[ \dfrac{3}{2}(r_1)^2\sqrt{3}\right] = 54 \sqrt{3} \ \ \tiny{\blacksquare} \end{matrix}\begin{matrix}Letra \ (B) \end{matrix}