Quando uma barra metálica se desloca num campo magnético, sabe-se que seus elétrons se movem para uma das extremidades, provocando entre elas uma polarização elétrica. Desse modo, é criado um campo elétrico constante no interior do metal, gerando uma diferença de potencial entre as extremidades da barra. Considere uma barra metálica descarregada, de de comprimento, que se desloca com velocidade constante de módulo num plano horizontal (veja figura), próximo à superfície da Terra.
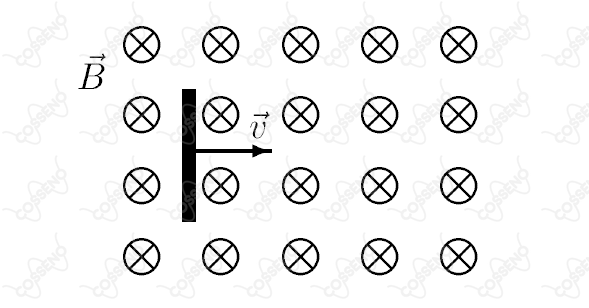
Sendo criada uma diferença de potencial (ddp) de entre as extremidades da barra, o valor do componente vertical do campo de indução magnética terrestre nesse local é de
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A partir do momento que a barra começa a se mover os elétrons sofrem uma força magnética, esta última provocando o acúmulo de carga numa extremidade da barra. Após isso, desenvolve-se uma diferença de potencial, o acúmulo de carga produz um campo elétrico, e assim há uma força elétrica contrária a magnética atuando nos elétrons. Nesse sentido, atingido o regime estacionário, têm-se:\begin{matrix}
F_{magnética} = F_{elétrica}
\end{matrix}Admitindo que o comprimento da barra seja $d$, têm-se:\begin{matrix}Bqv = Eq &\Rightarrow& B = \dfrac{E}{v} &\therefore& B =\dfrac{\Delta V}{vd}
\end{matrix}$\color{orangered}{\text{Obs:}}$ $\Delta V = E \cdot d$
Por fim, substituindo os dados do enunciado:\begin{matrix}B = \dfrac{(3 \cdot 10^{-3})}{60 \cdot 2} =2,5 \cdot 10^{-5} \ \pu{T} & \tiny{\blacksquare}
\end{matrix}\begin{matrix}Letra \ (C)
\end{matrix}$\color{orangered}{\text{Obs:}}$ $216 \ \pu{km/h} = 60\ \pu{m/s}$

