Um vagão-caçamba de massa se desprende da locomotiva e corre sobre trilhos horizontais com velocidade constante (portanto, sem resistência de qualquer espécie ao movimento). Em dado instante, a caçamba é preenchida com uma carga de grãos de massa igual a , despejada verticalmente a partir do repouso de uma altura de (veja figura).
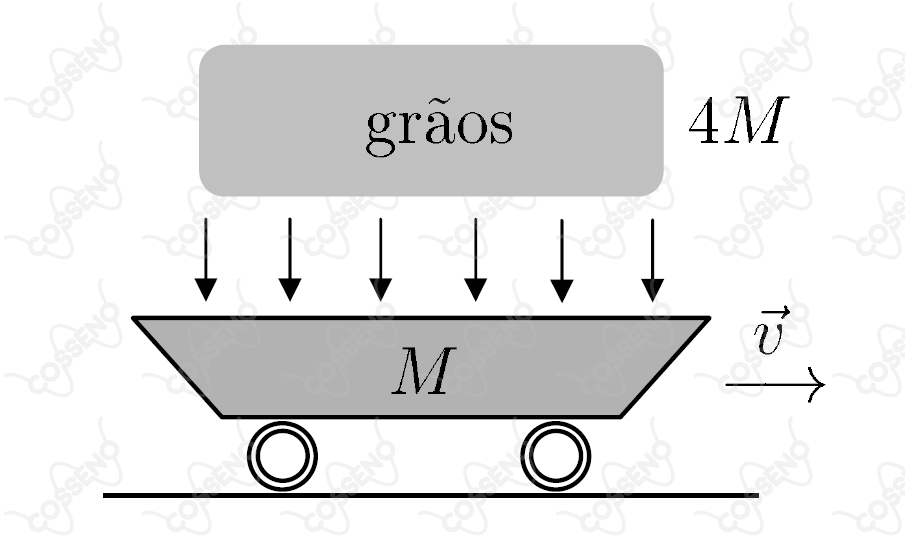
Supondo que toda a energia liberada no processo seja integralmente convertida em calor para o aquecimento exclusivo dos grãos, então, a quantidade de calor por unidade de massa recebido pelos grãos é
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Dado o enunciado entre parênteses, podemos assumir um sistema isolado na horizontal. Nessa perspectiva, vamos começar aplicando a conservação da quantidade de movimento, visto que ocorre variação de massa no carrinho:\begin{matrix}
p_{inicial} = p_{final} \\ M (20) +4M(0) = 5M(u) \\ \boxed{u =4 \ \pu{m/s}}
\end{matrix}$\color{orangered}{\text{Obs:}}$ $\pu{72 km/h = 20 m/s}$
Desse modo, como o sistema é conservativo, resta aplicar a conservação da energia mecânica, ou seja:\begin{matrix}
E_{M_{inicial}} = E_{M_{final}} \\
\dfrac{M(20)^2}{2} + 4Mg(6) = Q_T + \dfrac{5M(4)^2}{2} \\ \\ 200M + 240M = Q_T + 40M \\ \\ Q_T = 400M
\end{matrix}Repare que este é o calor total recebido pelos grãos, já para a quantidade de calor por unidade de massa, basta dividir pela massa total de grãos, veja:\begin{matrix}Q = \dfrac{Q_T}{4M} &\therefore& \boxed{Q = 100 \ \pu{J/kg}}
\end{matrix}\begin{matrix}Letra \ (C)
\end{matrix}

