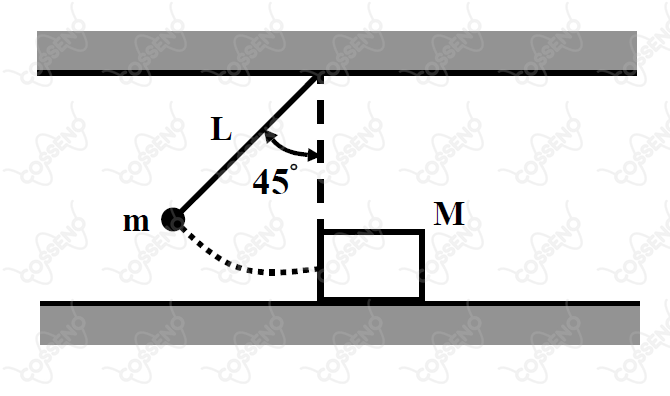
Quando solto na posição angular de (mostrada na figura), um pêndulo simples de massa e comprimento colide com um bloco de massa . Após a colisão, o bloco desliza sobre uma superfície rugosa, cujo coeficiente de atrito dinâmico é igual a . Considere que após a colisão, ao retornar, o pêndulo alcança uma posição angular máxima de .
Determine a distância percorrida pelo bloco em função de , e .
$$g = 9{,}8\ m/s^2$$
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A questão é um pouco longa e recomendo esboçar os passos, como não posso fazer isso, deixo com você esse trabalho. Além disso, serei pragmático em termos algébricos/geométricos da questão.
Adotando a posição mais baixa do pêndulo como nosso $Nível \ de \ Referência$, junto ao movimento horizontal para direita e vertical para cima como $Sentido \ Positivo$, temos:
Conservação da Energia Mecânica do pêndulo antes da colisão: \begin{matrix} mv_1^2 = mgL(2 - \sqrt{2}) \\ v_1 = \sqrt{gL(2 - \sqrt{2})} \\ \ \color{#3368b8}{(1)} \ \ \ \color{gray}{Note \ que, \ essa \ é \ a \ velocidade \ do \ pêndulo \ imediatamente \ antes \ da \ colisão.}\end{matrix}Conservação da Energia Mecânica do pêndulo após a colisão:\begin{matrix} mV_1^2 = mgL(2 - \sqrt{3}) \\ V_1 = - \sqrt{gL(2 - \sqrt{3})} \\ \ \color{#3368b8}{(2)} \ \ \color{gray}{Veja \ que, \ agora \ a \ velocidade \ está \ no \ sentido\ negativo, \ por \ isso \ o \ sinal \ de \ menos.}\\ \color{#3368b8}{(3)} \ \ \color{gray}{Repare \ que \ essa \ é \ a \ velocidade \ do \ pêndulo \ imediatamente \ após \ a \ colisão.}\end{matrix}Conservação da Quantidade de Movimento no impacto: \begin{matrix} mv_1 = mV_1 + MV_2&\Rightarrow&V_2 =\dfrac{m(v_1 - V_1)}{M}\end{matrix}Encontrando a aceleração do bloco de massa $M$ após a colisão:\begin{matrix} Ma = - fat &\Rightarrow& Ma = - μ_eMg&\Rightarrow& a= - μ_eg \end{matrix}Aplicando Torricelli para encontrar a distância: $(V^2 = V_0^2 + 2a\Delta S)$\begin{matrix} \Delta S = \dfrac{5m^2L(\sqrt{2 - \sqrt{2}} + \sqrt{2 - \sqrt{3}})^2}{3M^2}\end{matrix}

02:50 23/10/2021
Perdão, Augusto! Eu até percebi depois que enviei, mas não consigo editar, poderia fazer isso por mim?

01:26 23/10/2021
Pequeno erro na primeira equação: a velocidade está ao quadrado e o lado esquerdo possui denominador 1. A solução tirando essa parte está correta.

02:50 23/10/2021
Perdão, Augusto! Eu até percebi depois que enviei, mas não consigo editar, poderia fazer isso por mim?
