Esboçando a situação: 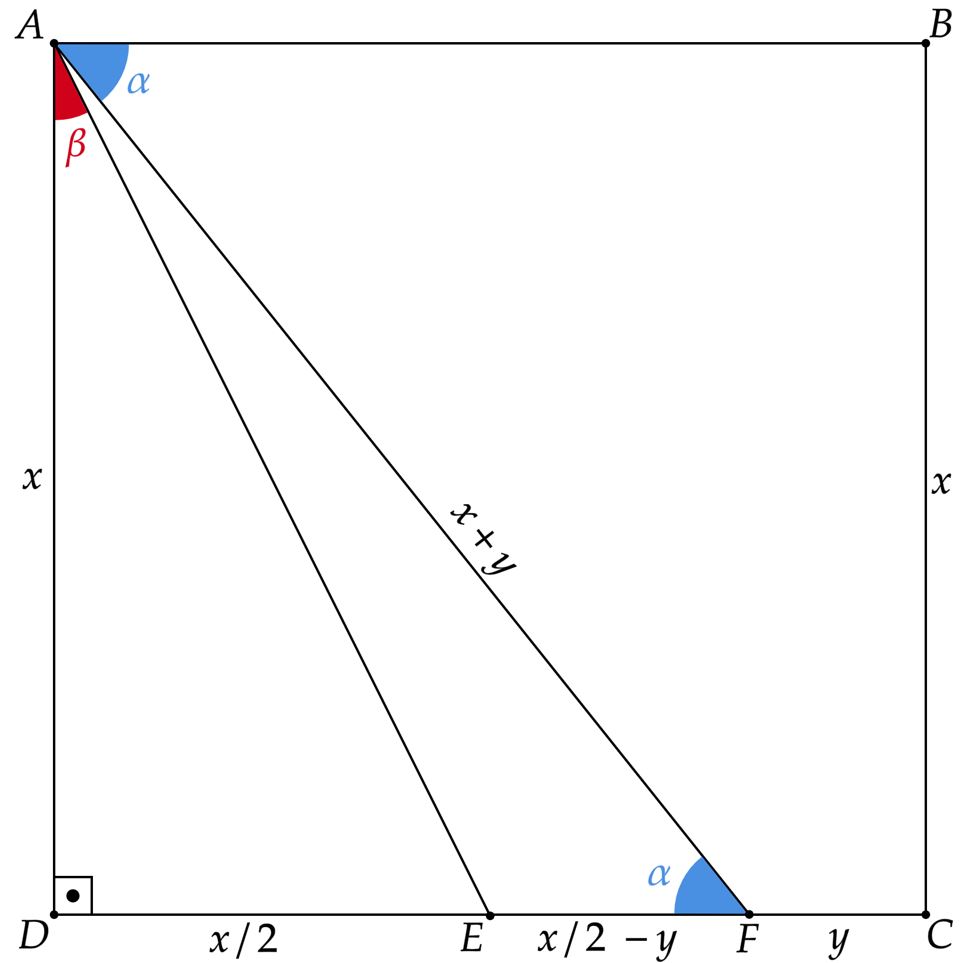Veja que podemos começar pensando em $\cos{\beta}$, assim, aplicando o teorema de Pitágoras no triângulo $ADE$:\begin{matrix} (\overline{AE})^2= x^2 + \left(\dfrac{x}{2}\right)^2 &\Rightarrow& \overline{AE} = \dfrac{\sqrt{5}}{2}x &\Rightarrow& \cos{\beta} = \dfrac{2}{\sqrt{5}} \end{matrix}Nesse sentido, vale lembrar que $\cos{2\beta} = 2\cos^2{\beta} - 1$, ou seja:\begin{matrix} \cos{2\beta} =2 \cdot \left(\dfrac{2}{\sqrt{5}} \right)^2 -1 &\therefore& \boxed{\cos{2\beta} = \dfrac{3}{5}} \end{matrix}Agora, para o $\cos{\alpha}$, pode-se começar aplicando o teorema de Pitágoras no triângulo $ADF$:\begin{matrix} (x+y)^2 = x^2 + (x-y)^2 \\ x =4y \end{matrix}Com isso,\begin{matrix} \cos{\alpha} = \dfrac{x-y}{x+y} &\therefore& \boxed{\cos{\alpha} = \dfrac{3}{5}} \end{matrix}Dessa forma, podemos inferir que:\begin{matrix} \boxed{\cos{\alpha} = \cos{2\beta}} & \tiny{\blacksquare} \end{matrix}