A priori, as esferas formam um tetraedro regular, isto é, três esferas formam a base - esferas tangentes duas a duas - enquanto a quarta esfera tangencia as três, estando acima das mesmas. Nessa perspectiva, o tetraedro circunscrito às esferas também é regular, denotemos sua aresta de $L$, a altura $H$, enquanto a altura do tetraedro menor é $h$, assim, podemos esboçar a situação abaixo: 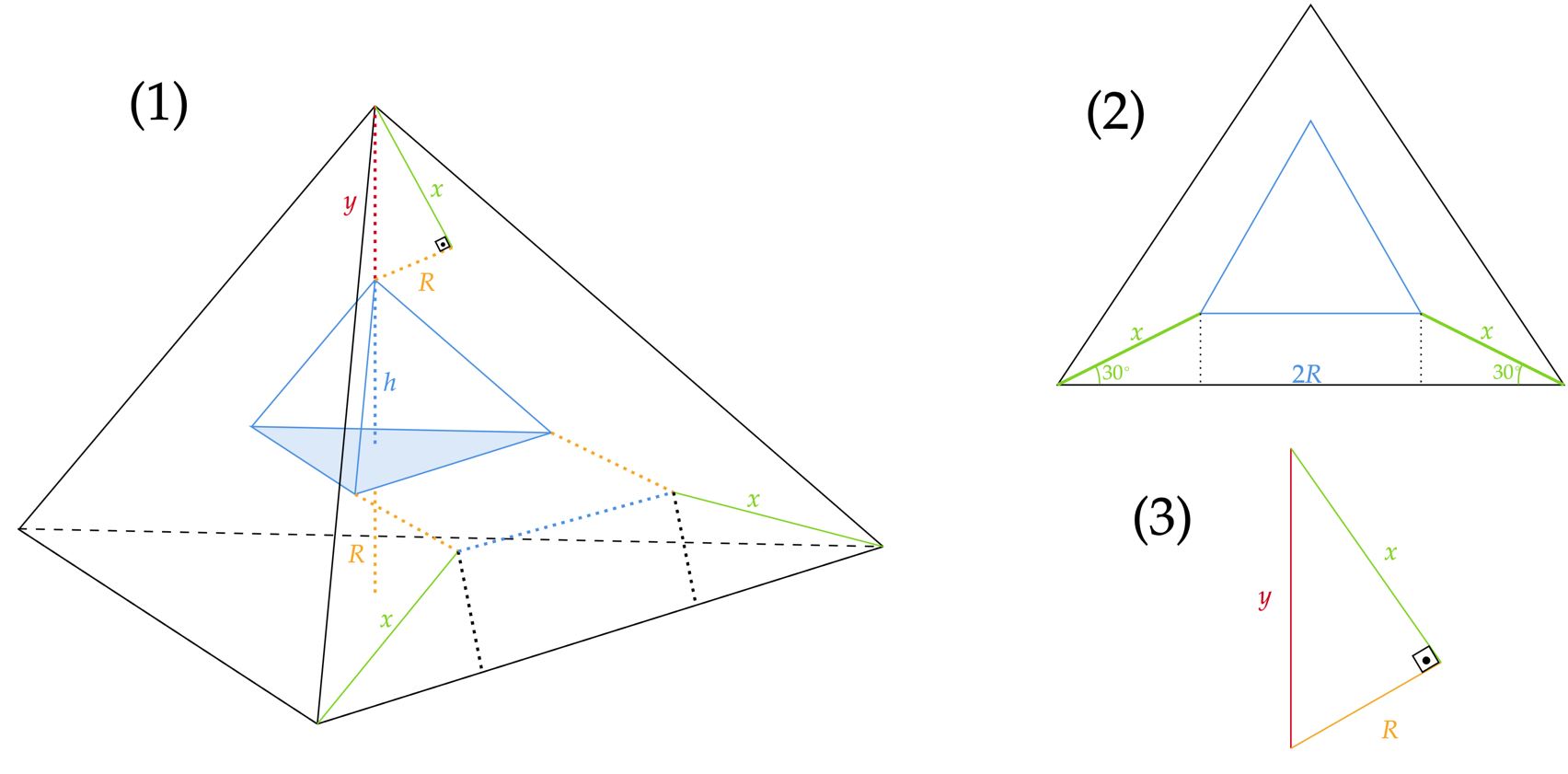Atente a figura $(1)$, as esferas obviamente foram omitidas para melhor compreensão. Com isso, repare em $x$, esta é a distância de um ponto de tangência ao vértice do tetraedro maior, é importante compreender a situação da imagem, pois a dificuldade da questão é justamente essa. Continuando, a altura do tetraedro maior é claramente: \begin{matrix} H = R + h + y \end{matrix}Veja que, queremos tudo em função de $R$, então comecemos encontrando a altura $h$. Nesse viés, para poupar o excesso de cálculos, a altura de um tetraedro regular é notável, esta que será: \begin{matrix} h = {{\dfrac{(2R)\sqrt{6}}{6}}} &\therefore& \fbox{$h = {{\dfrac{R\sqrt{6}}{3}}} $}\end{matrix}Agora, pela figura $(3)$: \begin{matrix} y^2 = R^2 + x^2 &\therefore& y = \sqrt{R^2 + x^2} \end{matrix}Então a altura do tetraedro maior:\begin{matrix} H = R + {{\dfrac{R\sqrt{6}}{3}}} + \sqrt{R^2 + x^2} \end{matrix} Como os dois tetraedros são regulares, podemos fazer uma semelhança entre seus respectivos lados e alturas. Contudo, antes de fazer essa semelhança, note a figura $(2)$, dela, a aresta $L$ do tetraedro será: \begin{matrix} L = 2R + 2(x\cos{30^{\circ}}) &\therefore& L= 2R + x\sqrt{3} \end{matrix}Desse modo, fazendo a semelhança:\begin{matrix} {{\dfrac{L}{2R}}} = {{\dfrac{H}{h}}} &\Rightarrow& x\sqrt{2} - R = \sqrt{R^2 + x^2} &\therefore& \fbox{$x = 2R\sqrt{2}$} \end{matrix}Conclui-se que, a aresta e altura do tetraedro maior são: \begin{matrix} \fbox{$L = 2R(1 + \sqrt{6})$} &\wedge& \fbox{$H = R {{ \left(\dfrac{12 + \sqrt{3}}{3} \right)}} $} \end{matrix}Portanto, o volume do tetraedro circunscrito às quatro esferas é: \begin{matrix} V = {{\dfrac{H}{3}}} \cdot {{ \left(\dfrac{L^2\sqrt{3}}{4} \right)}} &\therefore& V = {{\dfrac{2R^2\sqrt{2}(1+\sqrt{6})^2}{3}}} & \tiny{\blacksquare} \end{matrix}