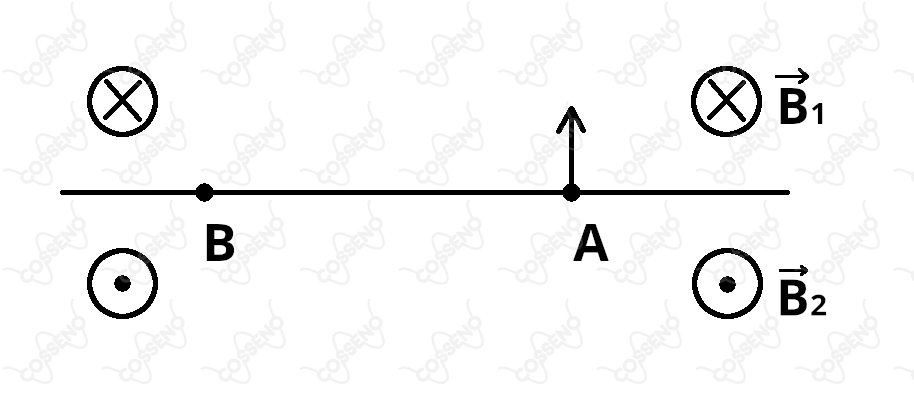
A figura mostra duas regiões nas quais atuam campos magnéticos orientados em sentidos opostos e de magnitude e , respectivamente. Um próton de carga e massa é lançado do ponto com uma velocidade perpendicular às linhas de campo magnético. Após um certo tempo , o próton passa por um ponto com a mesma velocidade inicial (em módulo, direção e sentido). Qual é o menor valor desse tempo?
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A priori, sabemos que a partícula chega em $B$ com a mesma velocidade inicial em módulo, sentido e direção. Dessa forma, devemos ter dois movimentos curvilíneos traçando uma semicircunferência cada, um no campo magnético $B_1$ e outro no campo $B_2$. Pela regra da mão direita, é notório o sentido da força magnética nos dois campos, força essa que atuará como resultante centrípeta, vejamos de forma geral:
\begin{matrix} |F_M|= |F_{cp}| &\Rightarrow& B\cdot q\cdot V = m\cdot \dfrac{V^2}{R} &\therefore& \fbox{$V=\dfrac{B\cdot q\cdot R}{m}$}
\end{matrix}
Como a partícula percorrerá uma semicircunferência, podemos escrever que: \begin{matrix} t =\dfrac{\pi R}{V}
&\therefore& \fbox{$t = \dfrac{m\cdot \pi}{B\cdot q}$}
\end{matrix} $\color{orangered}{Obs:}$ Se fosse uma circunferência inteira seria $2.\pi.R$, como é metade fica $\pi R$
Perceba que, pouco importa o raio da curva, iremos variar apenas o campo na nossa expressão acima, como teremos dois períodos, um em $B_1$ e outro em $B_2$ basta, escrever:
\begin{matrix} t_1 = \dfrac{m\cdot \pi}{B_1\cdot q} &,& t_2 = \dfrac{m\cdot \pi}{B_2\cdot q} \end{matrix} \begin{matrix} t_1 + t_2 = \dfrac{m\cdot \pi}{q}\cdot \left(\dfrac{1}{B_1}+\dfrac{1}{B_1}\right) &\therefore&
\fbox{$t_1 + t_2 = \dfrac{m\cdot \pi}{q}\cdot \left(\dfrac{B_1 + B_2}{B_1.B_2}\right)$} \\ \\ & Letra \ (A)&
\end{matrix}

