Pensando na situação descrita, pode-se encontrar o esboço abaixo: 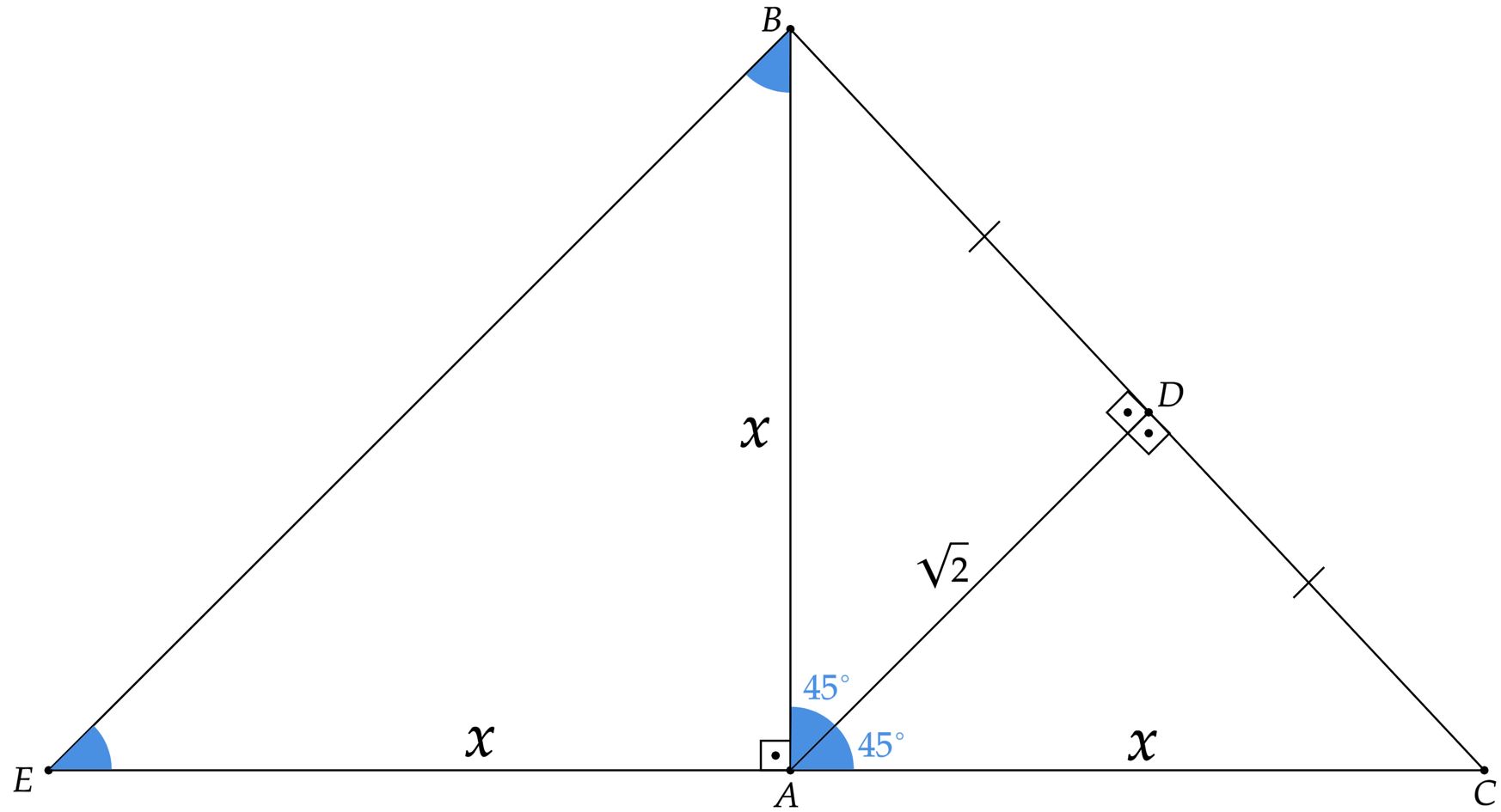A priori, sabemos que o triângulo é isósceles, ou seja, $\overline{AB} = \overline{AC}$. Além disso, sabemos que o segmento $ \overline{AD}$ é paralelo ao segmento $\overline{BE}$, consequentemente, $\angle{BAC} = \angle{BEA}$, isto é, o triângulo $ABE$ também é isósceles, em que $\overline{AC} = \overline{AE}$. Nesse sentido, não é difícil perceber que os triângulos $ABC$ e $ABE$ são iguais pelo critério $\text{Lado-Ângulo-Lado}$, por conseguinte, $\overline{BE} = \overline{BC}$. Posto tudo isso em mente, pode-se analisar o triângulo $ADC$, em que: \begin{matrix} \sin{45º} = \dfrac{\sqrt{2}}{2} = \dfrac{\sqrt{2}}{x} &\therefore& x = \sqrt{2} \end{matrix}Utilizando o $\text{Teorema de Pitágoras}$ no triângulo $ABC$, encontramos a hipotenusa, tal que: \begin{matrix} \overline{BC}^2 = \overline{BE}^2 = x^2 + x^2 &\therefore& \overline{BC} = \overline{BE} =2\sqrt{2} \end{matrix}Agora, é possível encontrar o raio $r$ do círculo inscrito a partir de uma relação de áreas, em que:\begin{matrix} \dfrac{\overline{AB} \cdot \overline{CE}}{2} = r \cdot p &,& p:\ \text{semi-perímetro} &|& p = 4(1+\sqrt{2}) \end{matrix}Continuando,\begin{matrix} r \cdot 4(1+\sqrt{2}) = x^2&\Rightarrow& r = 2(\sqrt{2} -1 ) \end{matrix}Então a área do círculo $S$ é:\begin{matrix} S = \pi \cdot r^2 &\therefore& S = 4\pi (3 - 2\sqrt{2}) \ \pu{cm^2} &\tiny{\blacksquare} \end{matrix}\begin{matrix}Letra \ (D) \end{matrix}$\color{#3368b8}{\text{Adendo:}}$ Mesmo que não fosse informado o fato de $ABC$ ser isósceles, ainda seria possível resolver, consequentemente, constatar que o mesmo deve ser isósceles.