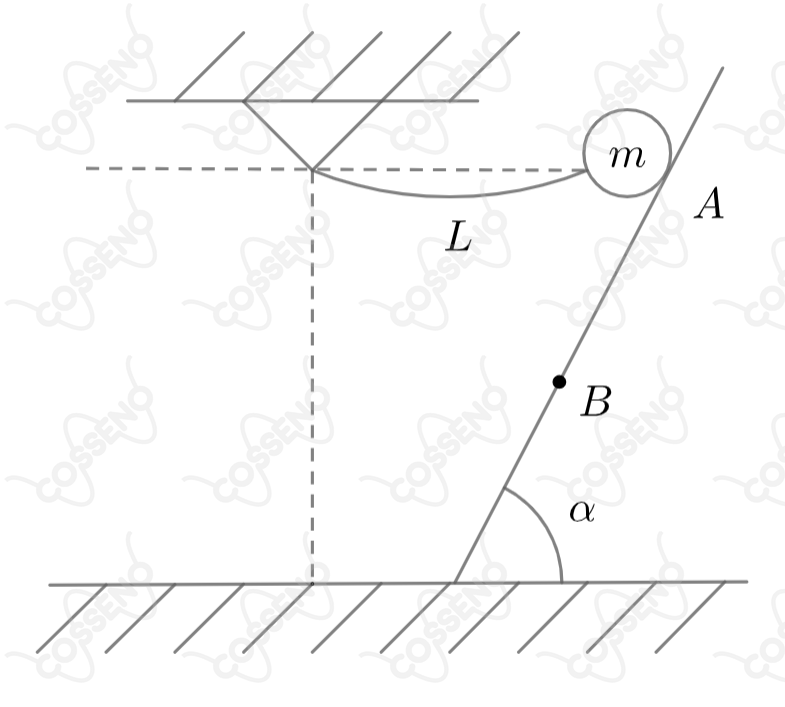
Um pêndulo é constituído por uma partícula de massa suspensa por um fio de massa desprezível, flexível e inextensível, de comprimento . O pêndulo é solto a partir do repouso, na posição , e desliza sem atrito ao longo de um plano de inclinação , como mostra a figura. Considere que o corpo abandona suavemente o plano no ponto , após percorrer uma distância sobre ele. A tração no fio, no instante em que o corpo deixa o plano, é:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Começando pela análise de quando o corpo do pêndulo está no ponto $B$, momento este que o corpo está na iminência de perder o contato, temos:
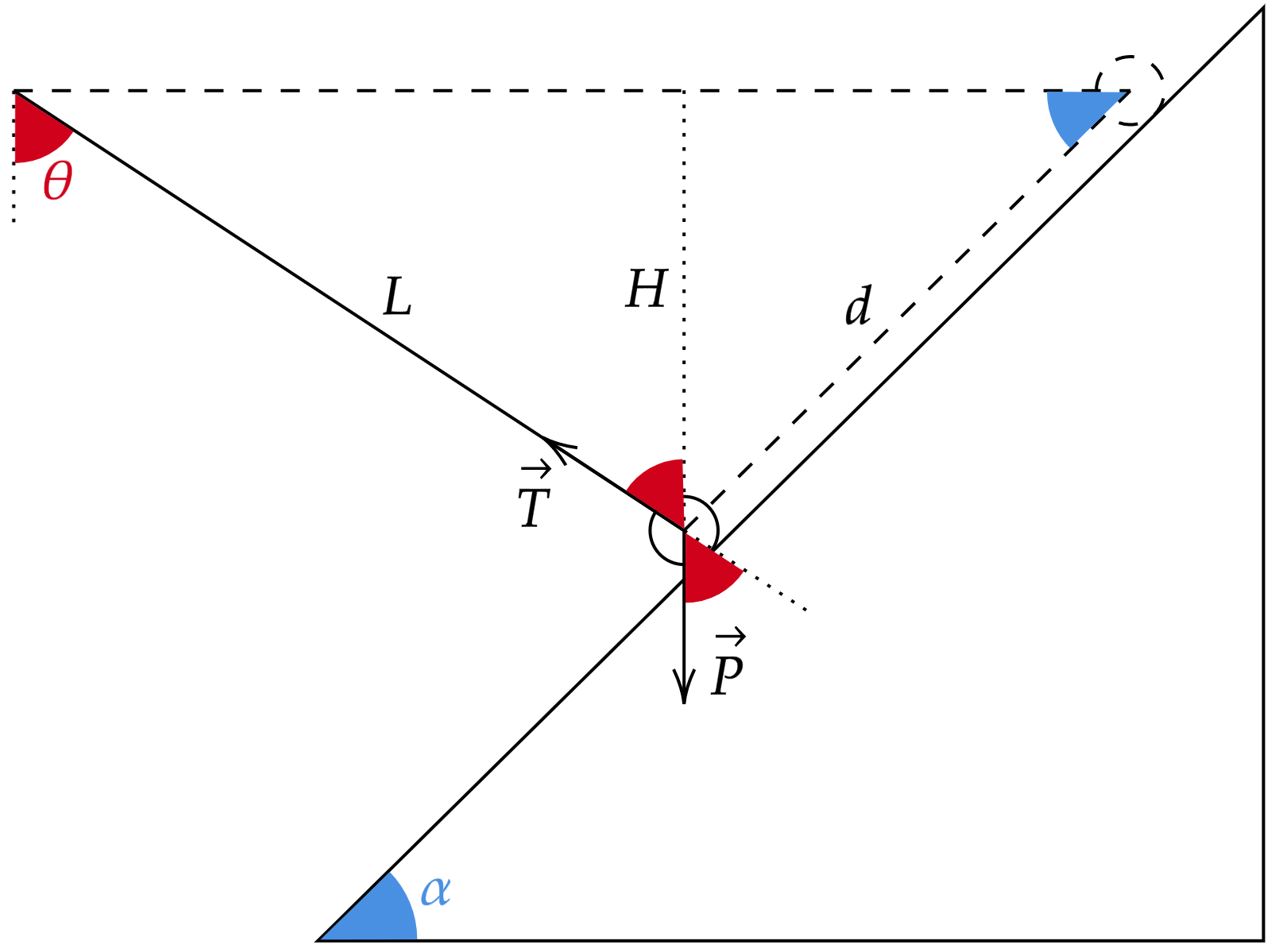 Observe que no momento de iminência o corpo começa a percorrer uma trajetória circular, analisando este movimento, constatamos:\begin{matrix}F_{cp} = T - P\cos{\theta} &\Rightarrow& T =\dfrac{mV^2}{L} + mg\cos{\theta} &(1)
\end{matrix}Note que existem termos a serem trabalhados, podemos partir do $\cos{\theta}$, este que pode ser escrito como:\begin{matrix} \cos{\theta} = \dfrac{H}{L} &,& H = d \sin{\alpha} &\therefore& \cos{\theta} = \dfrac{d \sin{\alpha}}{L} & (2)
\end{matrix}Nesse sentido, ainda falta encontrar a velocidade com que o corpo chega no ponto $B$, para isso, podemos utilizar a conservação da energia mecânica. No caso, tomando o ponto $B$ como o nível de referência, têm-se:\begin{matrix}\Delta E_M = 0 &\Rightarrow& mgH = \dfrac{mV^2}{2} &\therefore&mV^2 = 2mg( d\sin{\alpha}) & (3)
\end{matrix}Substituindo os resultados $(2)$ e $(3)$ em $(1)$, encontramos:\begin{matrix}T = 3mg \left(\dfrac{d}{L}\right)\sin{\alpha} & \tiny{\blacksquare}
\end{matrix}\begin{matrix}Letra \ (C)
\end{matrix}
Observe que no momento de iminência o corpo começa a percorrer uma trajetória circular, analisando este movimento, constatamos:\begin{matrix}F_{cp} = T - P\cos{\theta} &\Rightarrow& T =\dfrac{mV^2}{L} + mg\cos{\theta} &(1)
\end{matrix}Note que existem termos a serem trabalhados, podemos partir do $\cos{\theta}$, este que pode ser escrito como:\begin{matrix} \cos{\theta} = \dfrac{H}{L} &,& H = d \sin{\alpha} &\therefore& \cos{\theta} = \dfrac{d \sin{\alpha}}{L} & (2)
\end{matrix}Nesse sentido, ainda falta encontrar a velocidade com que o corpo chega no ponto $B$, para isso, podemos utilizar a conservação da energia mecânica. No caso, tomando o ponto $B$ como o nível de referência, têm-se:\begin{matrix}\Delta E_M = 0 &\Rightarrow& mgH = \dfrac{mV^2}{2} &\therefore&mV^2 = 2mg( d\sin{\alpha}) & (3)
\end{matrix}Substituindo os resultados $(2)$ e $(3)$ em $(1)$, encontramos:\begin{matrix}T = 3mg \left(\dfrac{d}{L}\right)\sin{\alpha} & \tiny{\blacksquare}
\end{matrix}\begin{matrix}Letra \ (C)
\end{matrix}

Ampliar Imagem

