Seja $z = (x,y)$, assim:\begin{matrix} |z + 1 + i |^2 &=& (x+1)^2 + (y+1)^2 &,& | |z| - |1+i||^2 &=& |\sqrt{x^2+y^2} - \sqrt{2}|^2 &=& (\sqrt{x^2+y^2} - \sqrt{2})^2 \end{matrix}Segundo enunciado,\begin{matrix} (x+1)^2 + (y+1)^2 &=& (\sqrt{x^2+y^2} - \sqrt{2})^2 \end{matrix} \begin{matrix} x&+&y &=& -\sqrt{2(x^2+y^2)} & \color{royalblue}{(1)} \end{matrix}Elevando $(1)$ ao quadrado, temos:\begin{matrix} (x-y)^2 = (y-x)^2 = 0 &\Rightarrow& \fbox{$x=y$} \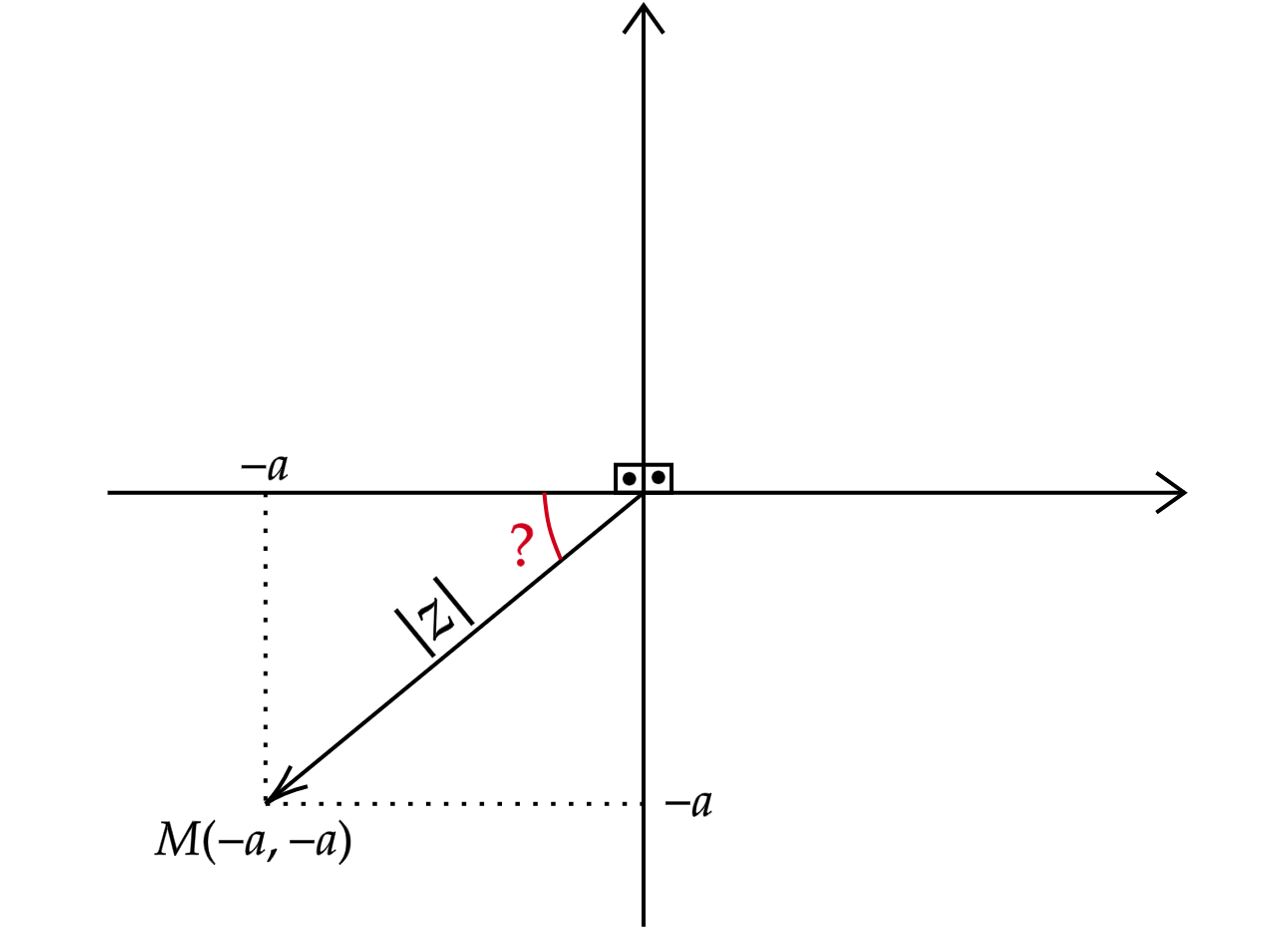end{matrix}Veja que, o resultado $(1)$ implica $x , y \ < \ 0$ , isto é, o nosso complexo é na forma $z = (-a , -a)$, o que garante $z$ no terceiro quadrante, com argumento $(\varphi)$ como: \begin{matrix}\varphi = \pi \ + \ ? &,& \tan{(?)} = \dfrac{x}{x} = 1 &\Rightarrow& ? = \dfrac{\pi}{4} \end{matrix}Portanto,\begin{matrix} \varphi &=& \dfrac{5\pi}{4} + 2k\pi \end{matrix} \begin{matrix} Letra \ (A) \end{matrix} $\color{orangered}{Obs:}$ Representação geométrica