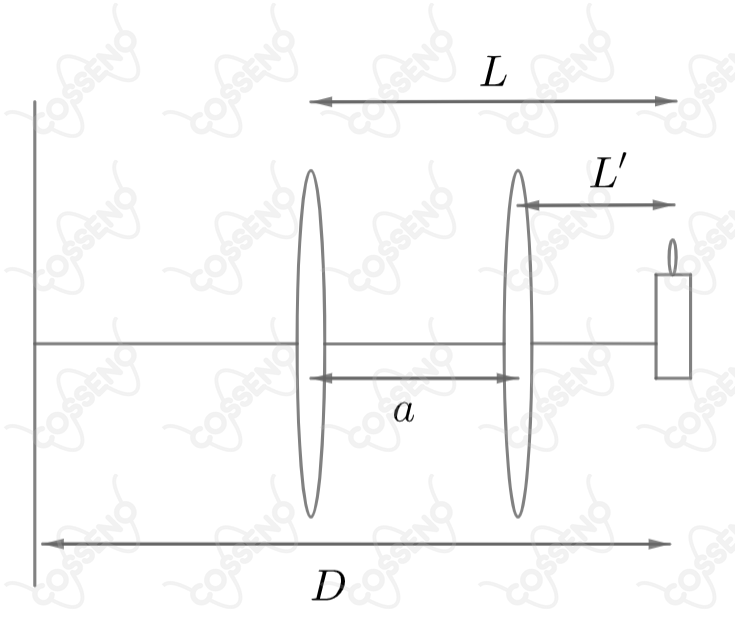
Uma vela está a uma distância de um anteparo sobre o qual se projeta uma imagem com lente convergente. Observa-se que as duas distâncias e entre a lente e a vela para as quais se obtém uma imagem nítida da vela no anteparo, distam uma da outra de uma distância . O comprimento focal da lente é então:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A questão requer apenas o conhecimento acerca da $\text{Equação de Gauss}$, assim, aplicando para os dois casos, temos: \begin{matrix} (1): &&& {\dfrac{1}{f} = \dfrac{1}{L-a} + \dfrac{1}{D-L+a}} &\Rightarrow& {\dfrac{1}{f} = \dfrac{D}{(L-a)(D-L+a)}} \\ \\
(2): &&& {\dfrac{1}{f} = \dfrac{1}{L} + \dfrac{1}{D-L}} &\Rightarrow& {\dfrac{1}{f} = \dfrac{D}{(L)(D-L)}}
\end{matrix}Igualando $(1)$ e $(2)$:\begin{matrix} (L-a)(D-L+a) = (L)(D-L) &\Rightarrow& \fbox{$L = {\dfrac{D+a}{2}}$} &,& a \ne 0
\end{matrix}Portanto, substituindo nosso resultado na equação $(2)$, encontramos:\begin{matrix} \fbox{$f = {\dfrac{D^2 - a^2}{4D}}$} \\ \\ Letra \ (D)
\end{matrix}

