Considere a hipérbole e a parábola , cujas equações são, respectivamente, Então, o lugar geométrico dos pontos , cuja soma dos quadrados das distâncias de a cada um dos fócos da hipérbole é igual ao triplo do quadrado da distância de ao vértice da parábola , é:
CossenoGPT
Teste gratuitamente agora mesmo! 
Ao reescrever a equação da hipérbole: \begin{matrix} \dfrac{(y-2)^2}{(\sqrt{5})^2} - \dfrac{(x+3)^2}{(2)^2} =1 &\Rightarrow& C: (-3,2)
\end{matrix} Conhecido o centro $C$, além de claro os eixos real e imaginário, ao aplicar a equação fundamental da hipérbole, encontraremos a distância focal $(c)$: \begin{matrix} c^2 = 5+4 &\therefore& c = 3
\end{matrix} Visto as coordenadas do centro, e sabido que a hipérbole apresenta abertura norte-sul, os focos devem estar em: \begin{matrix} F_1: (-3,5) &,& F_2: (-3,-1)
\end{matrix}
Agora, aplicando a $\text{Distância Euclidiana}$ entre os pontos $P:(a,b)$ , $F_1$ e $F_2$, têm-se:
\begin{matrix} (\overline{PF_1})^2 = (a +3)^2 + (b -5)^2 &,& (\overline{PF_2})^2 = (a +3)^2 + (b+1)^2
\end{matrix}
$-$ Continuando, pela parábola $T$ podemos identificar o vértice $V:(1,3)$. Novamente, aplicando $\text{Distância Euclidiana}$ :
\begin{matrix} (\overline{PV})^2 = (a -1)^2 + (b -3)^2
\end{matrix} $-$ Segundo enunciado, existe a relação: \begin{matrix} (\overline{PF_1})^2 + (\overline{PF_2})^2 = 3 (\overline{PV})^2 &\Rightarrow& a
^2 + b^2 - 18a - 10b - 14 = 0
\end{matrix}
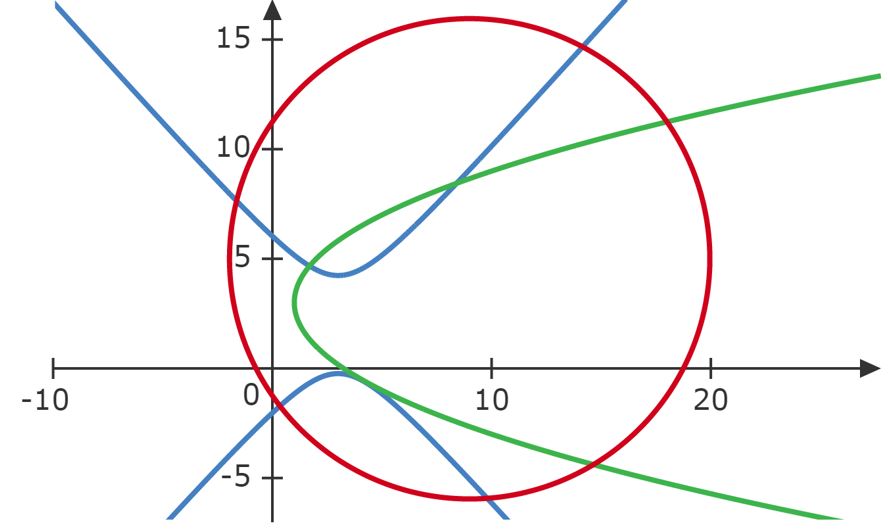
Portanto, constatamos a equação de uma circunferência, de centro $O: (9,5)$ e raio $R = \sqrt{120}$ , sendo sua equação reduzida:
\begin{matrix} (a -9)^2 + (b-5)^2 = (\sqrt{120})^2
\end{matrix}
\begin{matrix} Letra \ (E)
\end{matrix}
Ampliar Imagem
