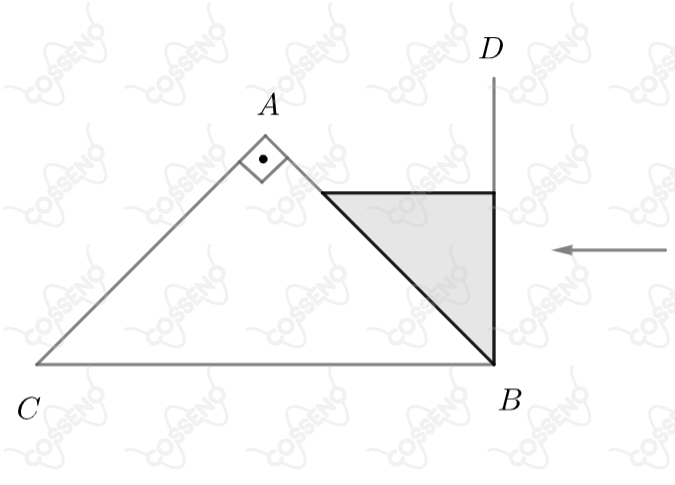
Um prisma de vidro, de índice de refração $n = (2)^{1/2}$, tem por secção normal um triângulo retângulo isósceles $ABC$ no plano vertical. O volume de secção transversal $ABD$ é mantido cheio de um líquido de índice de refração $n’ = (3)^{1/2}$. Um raio incide normalmente à face transparente da parede vertical $BD$ e atravessa o líquido. Considere as seguintes afirmações:
I- O raio luminoso não penetrará no prisma.
II- O ângulo de refração na face $AB$ é de $45^{\circ}$.
III- O raio emerge do prisma pela face $AC$ com ângulo de refração de $45^{\circ}$.
IV- O raio emergente definitivo é paralelo ao raio incidente em $BD$.
Das afirmativas mencionadas, é(são) correta(s):
$• \ \text{Afirmativa I:}$ $\color{orangered}{\text{Incorreta}}$
A priori, veja que o raio incide perpendicularmente ao "plano" $BD$, o que caracteriza não haver desvio na refração. Por conseguinte, o raio incide paralelo ao "plano" $BC$, informação essa que usaremos para descobrir o ângulo de incidência $(i_1)$, em vista do enunciado informar que o prima é um triângulo isósceles e triângulo, assim $i_1 = 45^°$. Dessa forma, nós precisamos apenas conferir se este é o ângulo crítico, pois do contrário, o raio poderá penetrar o prisma, com isso, sabida a $\text{Lei de Snell-Descartes}$:
\begin{matrix} {\dfrac{\sin{i_1}}{\sin{r_1}} = \dfrac{n^{`}}{n}} &\Rightarrow& \sin{r_1} = {\dfrac{\sqrt{3}}{2}} &\Rightarrow& \fbox{$r_1 = 60^°$}
\end{matrix} Assim, temos que o raio irá penetrar o prisma, pois para o ângulo crítica deveríamos ter $r_1 = 90^{°}$
$\color{orangered}{Obs:}$ Utilize a propriedade dos ângulos alternos internos para descobrir o ângulo de incidência.
$• \ \text{Afirmativa II:}$ $\color{orangered}{\text{Incorreta}}$
Vide a explicação anterior.
$• \ \text{Afirmativa III:}$ $\color{royalblue}{\text{Correta}}$
Com conhecimento que o ângulo de abertura é $90^{°}$ temos:
\begin{matrix} 90^{°} = r_1 + r_2 &\Rightarrow& \fbox{$r_2 = 30^{°}$}
\end{matrix}Portanto, podemos aplicar novamente a $\text{Lei de Snell-Descartes}$:\begin{matrix} {\dfrac{\sin{i_2}}{\sin{r_2}} = \dfrac{n}{n_{ar}}} &\Rightarrow& \sin{i_2} = {\dfrac{\sqrt{2}}{2}} &\Rightarrow& \fbox{$i_2 = 45^°$}
\end{matrix} $\color{orangered}{Obs:}$ $n_{ar} \approx 1$
$• \ \text{Afirmativa IV:}$ $\color{royalblue}{\text{Correta}}$
Vide o resultado anterior.\begin{matrix} Letra \ (D)
\end{matrix}
