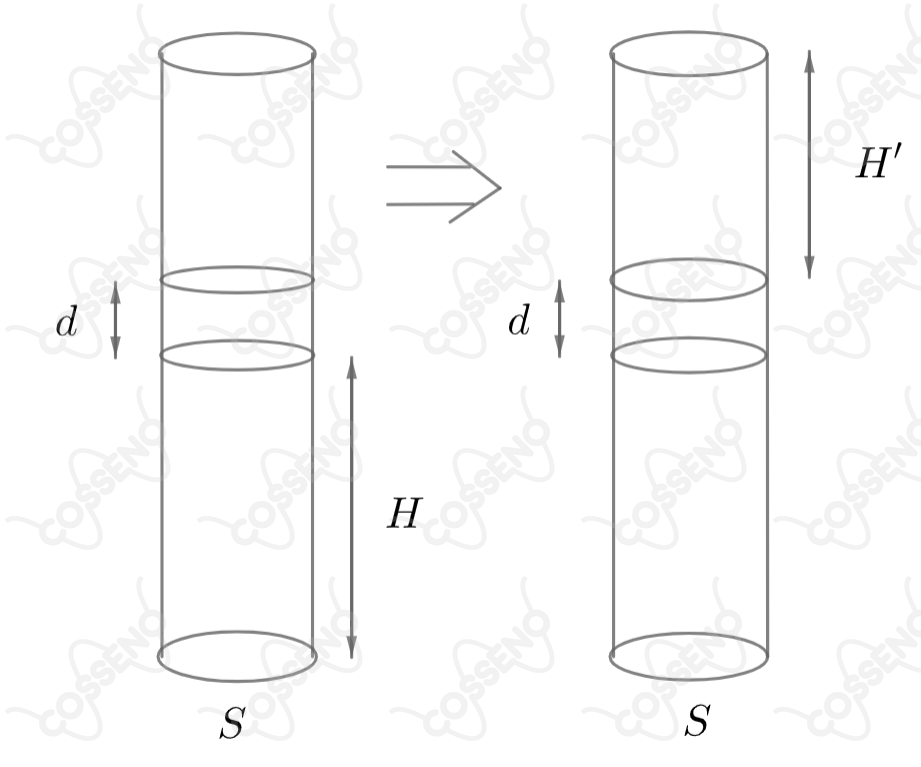
Um tubo vertical de secção , fechado em uma extremidade, contém um gás, separado da atmosfera por um êmbolo de espessura e massa específica . O gás, suposto perfeito, está à temperatura ambiente e ocupa um volume (veja figura). Virando o tubo tal que a abertura fique voltada para baixo, o êmbolo desce e o gás ocupa um novo volume, . Denotando a pressão atmosférica por , a nova altura é :
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Pressão exercida pelo gás na situação inicial: \begin{matrix} F_{gás} = Peso + F_{atm} \\ \\ P_{gás}\cdot S = Mg + P_{0}S \\ \color{gray}{\fbox{$\rho = \dfrac{M}{V}$}} \\ P_{gás}S = \rho \cdot d \cdot S\cdot g + P_{0}S \\ \\ \fbox{$P_{gás} = \rho\cdot d \cdot g + P_{0}$}
\end{matrix}Pressão exercida pelo gás na situação final: \begin{matrix} F _{f}= F_{atm} - Peso \\ \\ P_{f} S = P_{0}S - Mg \\ \color{gray}{\fbox{$\rho = \dfrac{M}{V}$}} \\ P_{f}S = P_{0}S - \rho\cdot d\cdot S\cdot g \\ \\ \fbox{$P_{f} = P_{0} - \rho\cdot d\cdot g $}
\end{matrix}Considerando a situação como uma transformação isotérmica, isto é, a temperatura constante, temos: \begin{matrix} PV = cte \\ \\ P_{gás}V = P_{f}V^′ \end{matrix}\begin{matrix}
( \rho\cdot d\cdot g + P_{0}) \cdot S\cdot H &=& ( P_{0} - \rho\cdot d\cdot g) \cdot S\cdot H^′
\end{matrix}\begin{matrix}{\fbox{$ H^′ = H\cdot \dfrac{ \rho\cdot d\cdot g + P_{0}}{ P_{0} - \rho\cdot d\cdot g} $}}
\end{matrix}\begin{matrix} Letra \ (E)
\end{matrix}

