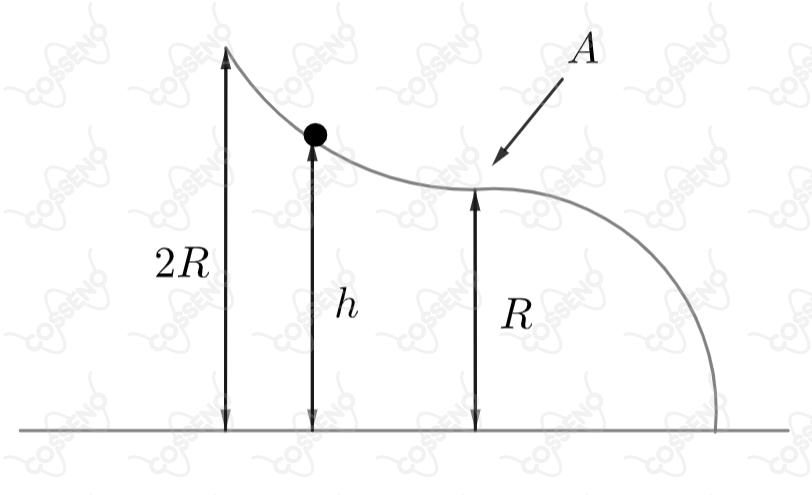
Um pequeno bloco, solto com velocidade nula a uma altura , move-se sob o efeito da gravidade e sem atrito sobre um trilho em forma de dois quartos de circulo de raio que se tangenciam, como mostra a figura. A mínima altura inicial que acarreta a saída do bloco, do trilho, após o ponto é:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Conservação da Energia Mecânica do ponto de partida até o ponto $A$ \begin{matrix} mgh = mgR + {{\dfrac{mV^2}{2}}} &\Rightarrow& V^2 = 2g(h-R)
\end{matrix}Analisando o bloco no ponto $A$, podemos dizer que: \begin{matrix} F_{cp} = P -N
\end{matrix}Para o bloco sair dos trilhos no ponto $A$, sua normal deve ser numericamente igual a zero, assim: \begin{matrix} m \cdot {{\dfrac{V^2}{R}}} = mg &\Rightarrow& V^2 =Rg &\Rightarrow& 2g(h-R) = Rg &\therefore& \fbox{ $h = \dfrac{3R}{2}$}
\end{matrix}\begin{matrix} Letra \ (C)
\end{matrix}

