O comprimento da diagonal de um pentágono regular de lado medindo unidade é igual à raiz positiva de: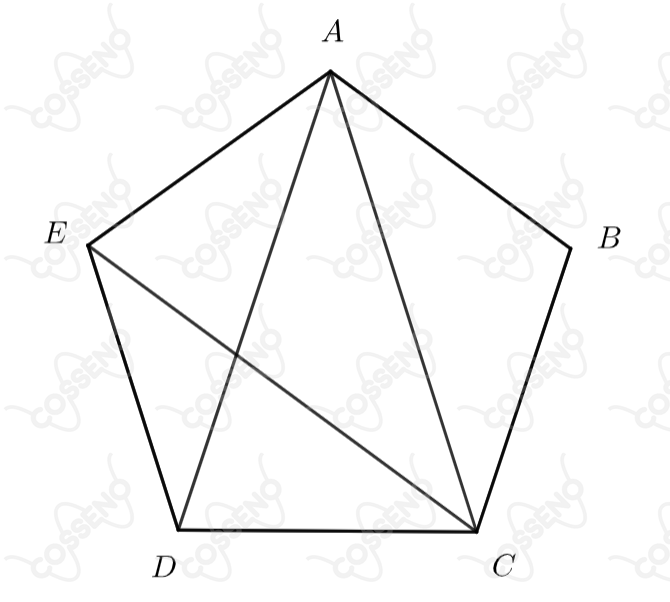
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A priori, é importante saber que todo polígono regular é inscritível, assim, temos:
$• \ \text{Resolução I:}$ Veja que, a imagem da questão já faz uma boa parte do trabalho, se você conhece o $\text{Teorema de Ptolomeu}$, não restam dúvidas ao olhar o quadrilátero $ACDE$, denotemos por $x$ a nossa diagonal:
\begin{matrix} x\cdot x = x\cdot 1 + 1\cdot 1 &\Rightarrow& \fbox{$x^2 - x - 1 = 0$}
\end{matrix}
$• \ \text{Resolução II:}$ Outra forma de resolver seria por semelhança de triângulos, primeiro, denotemos de $F$ o ponto de intersecção das diagonais na imagem, assim, atente aos triângulos isósceles $CDE$ , $DEF$ e $CDF$. Dessa forma, façamos a semelhança baseada nos triângulos $CDE$ e $DEF$:
\begin{matrix} { \dfrac{\overline{DE}}{\overline{EF}} = \dfrac{\overline{EC}}{\overline{DE}}} \\ \\ \color{gray}{\text{Como CDF é isósceles, $\overline{CF} = \overline{CD} = 1 $ , assim, $\overline{EF} = 1-x$}} \\ \\
{ \dfrac{1}{1-x} = \dfrac{x}{1} } \\ \\ \fbox{$x^2 - x - 1 = 0$}
\end{matrix}
$• \ \text{Resolução III:}$ Uma resolução pouco efetiva, mas que também é uma saída, seria conhecer um dos ângulos de $18º$, $36º$, $72º$ ou $108º$, isto é, saber seu seno ou cosseno. Dessa forma, com conhecimento do ângulo interno do pentágono regular $(108º)$, poderíamos apenas aplicar uma lei dos cossenos no triângulo $CDE$:
• Encontrando o ângulo interno do pentágono regular pelo ângulo externo:\begin{matrix} n.\hat{e} = 360º \ , \ n = 5 \ \text{(um pentágono)} \\ \\ \hat{e} = 72º \\ \color{gray}{\text{Dessa forma, o ângulo externo é $108º$}}
\end{matrix}
• Aplicando a $\text{Lei dos Cossenos}$ no triângulo $CDE$: \begin{matrix} d^2 = 1^2 + 1^2 - 2.1.1.\cos{108º} \\ \\ \color{gray}{\fbox{$\cos{108^{\circ}} = \dfrac{1 - \sqrt{5}}{4}$}} \\ \\ { \fbox{$d = \dfrac{1 + \sqrt{5}}{2}$}}
\end{matrix}Agora, você teria de resolver as equações de segundo grau até encontrar a resposta: \begin{matrix} \fbox{$x^2 - x - 1 = 0$} \\ \\ Letra \ (E)
\end{matrix}
Utilizando o Teorema de Ptolomeu podemos escrever que
$AD \cdot EC = AE \cdot DC + ED\cdot AC$
Como $AD = EC = AC = x$ e $ AE = DC = ED = 1$ , temos portanto que
$x \cdot x = 1\cdot 1 + 1 \cdot x = x^2 = 1 + x$
$\implies \boxed{x^2 -x -1 = 0}$
$\textbf{Resposta : Alternativa E}$



