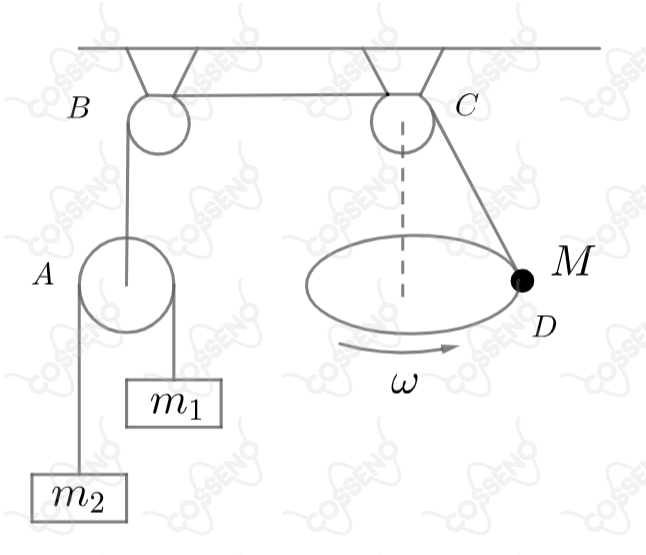
Um fio tem presa uma massa M numa das extremidades e na outra, uma polia que suporta duas massas; e unidas por um outro fio como mostra a figura. Os fios têm massas desprezíveis e as polias são ideais. Se e a massa gira com velocidade angular constante numa trajetória circular em torno do eixo vertical passando por , observa-se que o trecho do fio permanece imóvel. Considerando a aceleração da gravitacional , a massa deverá ser:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Começando pela polia, pode-se transformar as duas massas em uma massa resultante de modo que: \begin{matrix} M_r = {{\dfrac{4.m_1.m_2}{m_1 + m_2} }}&\Rightarrow& M_r = 3kg
\end{matrix}Como tudo está parado, a tração será igual ao peso da nossa massa resultante:\begin{matrix} T = M_r.g = 30N
\end{matrix}Perceba que a tração na polia é a mesma do objeto de massa $M$, assim, ao decompor a tração iremos focar na resultante centrípeta, veja: \begin{matrix} M.w^2.R= T.\cos{\alpha} &\Rightarrow& \cos{\alpha} = {{\dfrac{R}{0,80}}} &\therefore& \fbox{M= 1,5kg}
\end{matrix}\begin{matrix}Letra \ (D)
\end{matrix}$• \ \text{Demonstração:}$ $\color{royalblue}{\text{Massa resultante numa polia}}$
Vamos supor uma polia e dois blocos, conhecendo o vínculo geométrico, podemos escrever duas equações notáveis: \begin{matrix} \begin{cases} m_1.a = T - m_1.g \\ m_2.a = m_2.g - T \end{cases}
&\Rightarrow&
a = {{\dfrac{T-m_1.g}{m_1} }}= {{\dfrac{m_2.g - T}{m_2}}} &\therefore& T= {{\dfrac{2.m_1.m_2.g}{m_1+ m_2}}}
\end{matrix}Vamos chamar a tração da polia de $T_p$, assim: \begin{matrix} T_p = 2.T &\Rightarrow&T_p = M_p.g
\end{matrix}Assim, substituindo nossos resultados: \begin{matrix} T_p = {{\dfrac{4.m_1.m_2.g}{m_1+ m_2} }} &\therefore& \fbox{$M_p= {{\dfrac{4.m_1.m_2}{m_1+ m_2}}}$}
\end{matrix}
Seja $T$ a tração do fio que está presa à massa $M$ , $T_{2}$ a tração do fio que está presa à massa $m_{1}$ e massa $m_{2}$ , $\theta$ o ângulo que o fio $CD$ realiza com o eixo vertical que passa pelo centro da trajetória circular da massa $M$ , $R$ o raio da trajetória circular da massa $M$ e $a$ a aceleração dos blocos de massa $m_{1}$ e $m_{2}$.
Analisando as forças atuantes sobre a massa $M$ e o seu movimento podemos constatar que
$T \sin\theta = \dfrac{M \cdot (\omega \cdot R)^2}{R} =T \sin\theta = M \cdot \omega^2 \cdot R \implies T = \dfrac{M \cdot \omega^2 \cdot R}{\sin\theta}$
$ = \dfrac{M \cdot 5^2 \cdot R}{\left(\dfrac{R}{CD}\right)} = 25 \cdot M \cdot CD = T = 25 \cdot M \cdot 0,80 = \boxed{T = 20M} $
Analisando o sistema de polias podemos concluir que
$\begin{cases}
m_{1} \cdot g - T_{2} = m_{1} \cdot a \\
T_{2} - m_{2}\cdot g = m_{2} \cdot a
\end{cases} \implies g ( m_{1} - m_{2}) = a( m_{1}+ m_{2}) \implies a = \dfrac{g(m_{1} - m_{2})}{m_{1} + m_{2}}$
$a = \dfrac{10 \cdot 2}{4} = \boxed{a = 5 \text{ m}/\text{s}^2} $
$\therefore$
$T_{2} - m_{2}\cdot g = m_{2} \cdot a = T_{2} - 1 \cdot 10 = 1 \cdot 5 \implies \boxed{T_{2} = 15 \text{ N}}$
Note que $T = 2T_{2} $
$\therefore$
$T = 2 \cdot 15 = \boxed{T = 30 \text{ N}}$
$\therefore$
$20M = T = 20M = 30 \implies M = \dfrac{30}{20} = \boxed{M = 1,5 \text{ kg}}$
$\textbf{Resposta : Alternativa D}$



