Um fio de comprimento oferece resistência elétrica . As pontas foram soldadas formando um círculo. Medindo a resistência entre dois pontos que compreendam um arco de círculo de comprimento verificou-se que era . Dobrando o comprimento do arco a resistência será:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Segundo a situação do enunciado, podemos esboçar, a partir da $\text{Segunda Lei de Ohm}$, a figura abaixo:
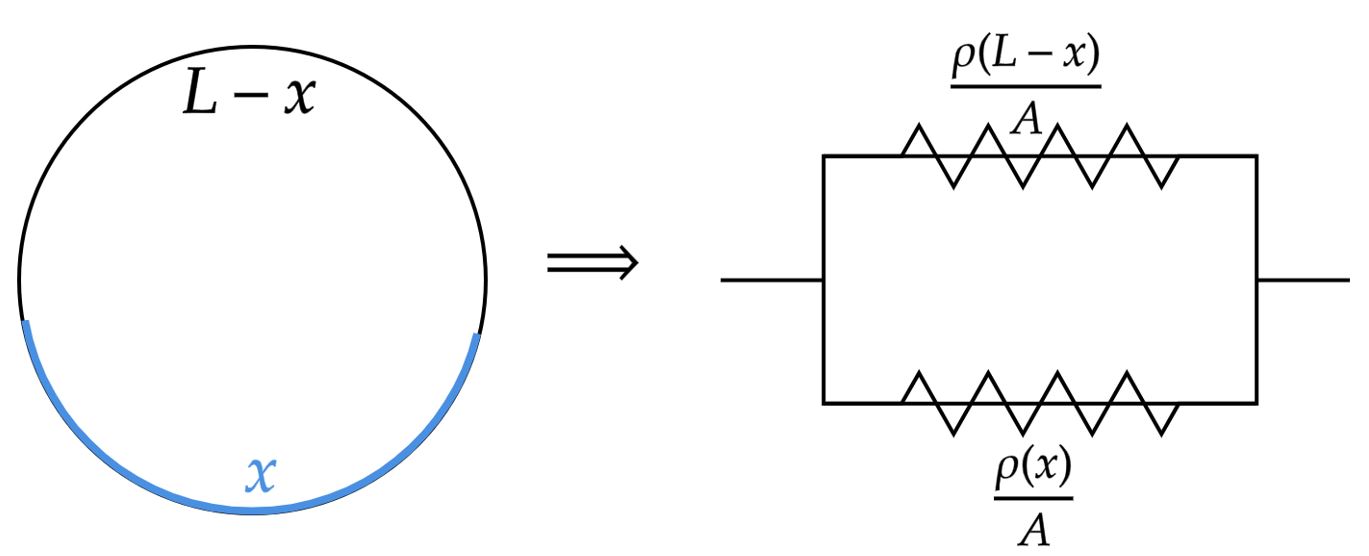 Veja que, temos uma associação em paralelo entre dois resistores, esta que possui resultante $R_1$, logo: \begin{matrix} R_1 = {\LARGE{ \frac{\frac{\rho x}{A}.\frac{\rho (L-x)}{A}}{\frac{\rho (x)}{A} + \frac{\rho (L-x)}{A}} }} = \Large{\frac{\rho x(L-x)}{A L}} &\therefore& {\Large{\frac{\rho}{A}}} = {\Large{\frac{R_i \ . \ L}{x(L-x)}}} = cte
\end{matrix}Assim, ao dobrar o comprimento temos $2x$, atente \begin{matrix} {\Large{\frac{R_1 \ . \ L}{x(L-x)}}} = {\Large{\frac{R_2 \ . \ L}{2x(L-2x)}}} &\therefore& \fbox{$R_2 = 2R_1 \ .\ \large{\frac{(L-2x)}{(L-x)}} $}
\end{matrix}\begin{matrix} Letra \ (B)
\end{matrix}
Veja que, temos uma associação em paralelo entre dois resistores, esta que possui resultante $R_1$, logo: \begin{matrix} R_1 = {\LARGE{ \frac{\frac{\rho x}{A}.\frac{\rho (L-x)}{A}}{\frac{\rho (x)}{A} + \frac{\rho (L-x)}{A}} }} = \Large{\frac{\rho x(L-x)}{A L}} &\therefore& {\Large{\frac{\rho}{A}}} = {\Large{\frac{R_i \ . \ L}{x(L-x)}}} = cte
\end{matrix}Assim, ao dobrar o comprimento temos $2x$, atente \begin{matrix} {\Large{\frac{R_1 \ . \ L}{x(L-x)}}} = {\Large{\frac{R_2 \ . \ L}{2x(L-2x)}}} &\therefore& \fbox{$R_2 = 2R_1 \ .\ \large{\frac{(L-2x)}{(L-x)}} $}
\end{matrix}\begin{matrix} Letra \ (B)
\end{matrix}

Ampliar Imagem

