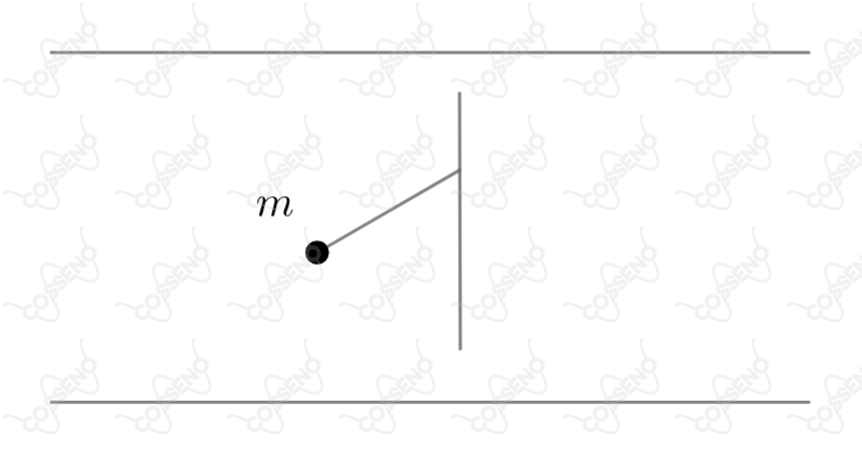
A figura mostra a secção transversal de um cilindro feito de um material cujo índice de refração é imerso num meio de índice . Os valores dos índices são e não necessariamente nessa ordem. Para que um feixe de luz contido no plano seccionador e proveniente do meio de índice penetre no cilindro mas não consiga escapar, devemos satisfazer às seguintes condições:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Analisemos primeiro o caso com $n_1=1$ e $n_2=\sqrt{2}$. Para descobrir o ângulo de refração $\sigma$, recorremos à lei de Snell-Descartes:$$n_1\sin{\theta}=n_2\sin{\sigma}$$$$\sin{\sigma}=\frac{\sqrt{2}}{2}\sin{\theta}$$Já dentro do cilindro, a direção normal à superfície sempre coincide com a direção radial, devido à natureza da circunferência. Sendo assim, o ângulo incidente na interface que o feixe encontra após penetrar no cilindro será também igual a $\sigma$.Para garantir que o feixe não seja capaz de sair do cilindro, devemos garantir que $\sigma$ seja maior que o ângulo crítico $\sigma_{c}$, a partir do qual ocorre reflexão interna total. Assim, determinamos $\sigma_c$:$$n_2\sin{\sigma_c}=n_1\sin{90^{\circ}}$$$$\sin{\sigma_c}=\frac{\sqrt{2}}{2}$$Dessa forma, ângulos $\sigma > 45^{\circ}$ não escaparão do cilindro.Mas uma vez que $\sin{\sigma}=\frac{\sqrt{2}}{2}\sin{\theta}$ e que $\sin{\theta}\in[0,1)$ para qualquer feixe que penetra o cilindro, então é sempre verdade que $\sin{\sigma}<\frac{\sqrt{2}}{2}$, e portanto, o feixe de luz sempre escapará na condição $n_1=1$ e $n_2=\sqrt{2}$.Analisando agora o caso com $n_1=\sqrt{2}$ e $n_2=1$, como o feixe passará de um meio mais refringente para um menos refringente, devemos primeiro verificar se não ocorre reflexão interna total, para garantir que o feixe entrará no cilindro. Todos os ângulos de incidência $\theta$ devem satisfazer à condição $\theta<\theta_c$, sendo o ângulo de incidência crítico calculado a seguir:$$n_1\sin{\theta_c}=n_2\sin{90^{\circ}}$$$$\sin{\theta_c}=\frac{\sqrt{2}}{2}$$Ou seja, somente com $\theta<45^{\circ}$ o feixe penetrará no cilindro. Agora, com o feixe entrando no cilindro, como a próxima refração será de um meio menos refringente para um meio mais refringente, inevitavelmente o feixe sairá do cilindro.Portanto, podemos que concluir que - para ambas as configurações de índices de refração e ângulos de incidência - não é possível fazer o feixe entrar no cilindro sem que ele escape. Gabarito (D)

